Straight Line and Pair of Straight Lines 1 Question 53
53.
For points $P=\left(x _1, y _1\right)$ and $Q=\left(x _2, y _2\right)$ of the coordinate plane, a new distance $d(P, Q)$ is defined by $d(P, Q)=\left|x _1-x _2\right|+\left|y _1-y _2\right|$.
Let $O=(0,0)$ and $A=(3,2)$. Prove that the set of points in the first quadrant which are equidistant (with respect to the new distance) from $O$ and $A$ consists of the union of a line segment of finite length and an infinite ray. Sketch this set in a labelled diagram.
$(2000,10 M)$
Show Answer
Solution:
- $d:(P, Q)=\left|x _1-x _2\right|+\left|y _1-y _2\right|$.
It is new method of representing distance between two points $P$ and $Q$ and in future very important in coordinate geometry.
Now, let $P(x, y)$ be any pont in the first quadrant. We have
$d(P, 0)$ $= |x-0 |+ |y-0| = |x| + |y |=x+y$
$[\because x, y>0]$
$d(P, A)$ $= |X-3| + |Y-2| $ [given]
$d(P, 0)$ $=d(P, A)$ [given]
$\Rightarrow \quad x+y$ $= |x-3| + |y-2| $ $\ldots(i)$
Case I When $0<x<3,0<y<2$
Case I When $0<x<3,0<y<2$
In this case, Eq. (i) becomes
$ x+y=3-x+2-y $
$ \begin{aligned} \Rightarrow & & 2 x+2 y & =5 \\ \text { or } & & x+y & =5 / 2 \end{aligned} $
Case II When $0<x<3, y \geq 2$
Now, Eq. (i) becomes
$ \begin{aligned} & x+y=3-x+y-2 \\ & \Rightarrow \quad 2 x=1 \\ & \Rightarrow \quad x=1 / 2 \end{aligned} $
Case III When $x \geq 3,0<y<2$
Now, Eq. (i) becomes
$ \begin{aligned} & x+y=x-3+2-y \\ & \Rightarrow \quad 2 y=-1 \quad \text { or } \quad y=-1 / 2 \end{aligned} $
Hence, no solution.
Case IV When $x \geq 3, y \geq 2$
In this case, case I changes to
$ x+y=x-3+y-2 \Rightarrow 0=-5 $
which is not possible.
Hence, the solution set is
$(x, y) \mid x=12, y \geq 2 \cup(x, y) \mid $
$ x+y=5/2,0< x <3,0 < y > 2 $
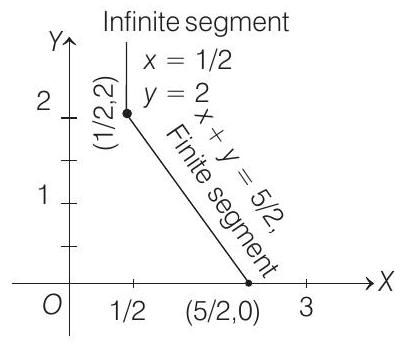
The graph is given in adjoining figure.
