Straight Line and Pair of Straight Lines 1 Question 53
53. For points $P=\left(x _1, y _1\right)$ and $Q=\left(x _2, y _2\right)$ of the coordinate plane, a new distance $d(P, Q)$ is defined by $d(P, Q)=\left|x _1-x _2\right|+\left|y _1-y _2\right|$.
Let $O=(0,0)$ and $A=(3,2)$. Prove that the set of points in the first quadrant which are equidistant (with respect to the new distance) from $O$ and $A$ consists of the union of a line segment of finite length and an infinite ray. Sketch this set in a labelled diagram. $(2000,10 M)$
Show Answer
Solution:
- NOTE $d:(P, Q)=\left|x _1-x _2\right|+\left|y _1-y _2\right|$.
It is new method of representing distance between two points $P$ and $Q$ and in future very important in coordinate geometry.
Now, let $P(x, y)$ be any pont in the first quadrant. We have
| $d(P, 0)$ | $=|x-0|+|y-0|=|x|+|y|=x+y$ | |
|---|---|---|
| $[\because x, y>0]$ | ||
| $d(P, A)$ | $=|X-3|+|Y-2|$ | [given] |
| $d(P, 0)$ | $=d(P, A)$ | [given] |
| $\Rightarrow \quad x+y$ | $=|x-3|+|y-2|$ | $\ldots(i)$ |
| Case I When $0<x<3,0<y<2$ |
Case I When $0<x<3,0<y<2$
In this case, Eq. (i) becomes
$$ x+y=3-x+2-y $$
$$ \begin{aligned} \Rightarrow & & 2 x+2 y & =5 \\ \text { or } & & x+y & =5 / 2 \end{aligned} $$
Case II When $0<x<3, y \geq 2$
Now, Eq. (i) becomes
$$ \begin{aligned} & x+y=3-x+y-2 \\ & \Rightarrow \quad 2 x=1 \\ & \Rightarrow \quad x=1 / 2 \end{aligned} $$
Case III When $x \geq 3,0<y<2$
Now, Eq. (i) becomes
$$ \begin{aligned} & x+y=x-3+2-y \\ & \Rightarrow \quad 2 y=-1 \quad \text { or } \quad y=-1 / 2 \end{aligned} $$
Hence, no solution.
Case IV When $x \geq 3, y \geq 2$
In this case, case I changes to
$$ x+y=x-3+y-2 \Rightarrow 0=-5 $$
which is not possible.
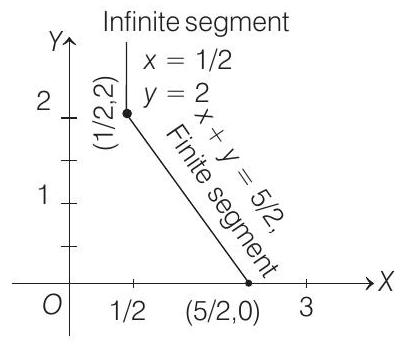
Hence, the solution set is
$$
\begin{aligned}
& {(x, y) \mid x=12, y \geq 2} \cup{(x, y)} \mid \\
& x+y=5 / 2,0<x<3,0
The graph is given in adjoining figure.
