Straight Line and Pair of Straight Lines 1 Question 51
51. A straight line $L$ through the origin meets the line $x+y=1$ and $x+y=3$ at $P$ and $Q$ respectively. Through $P$ and $Q$ two straight lines $L _1$ and $L _2$ are drawn, parallel to $2 x-y=5$ and $3 x+y=5$, respectively. Lines $L _1$ and $L _2$ intersect at $R$, show that the locus of $R$ as $L$ varies, is a straight line.
$(2002,5$ M)
Show Answer
Solution:
- Let the equation of straight line $L$ be
$Q \equiv \frac{3}{m+1}, \frac{3 m}{m+1}$
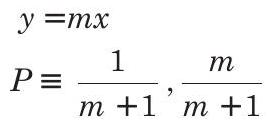
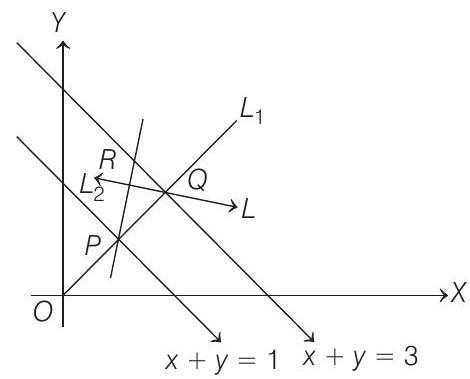
Now, equation of
$$ L _1: y-2 x=\frac{m-2}{m+1} $$
and equation of
$$ L _2: y+3 x=\frac{3 m+9}{m+1} $$
By eliminating $m$ from Eqs. (i) and (ii), we get locus of $R$ as $x-3 y+5=0$, which represents a straight line.
