Straight Line and Pair of Straight Lines 1 Question 51
51. A straight line
Show Answer
Solution:
- Let the equation of straight line
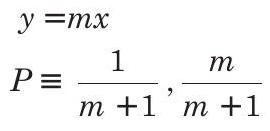
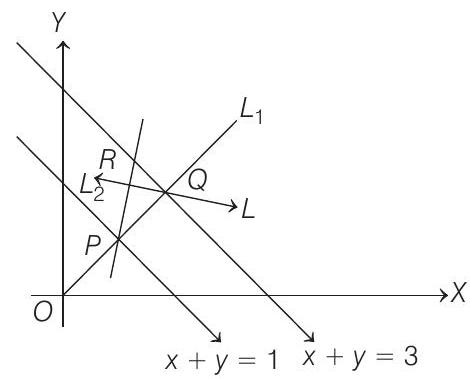
Now, equation of
and equation of
By eliminating






