SATHEE: Properties of Triangles 3 Question 17

Properties of Triangles 3 Question 17

17. Let $A B C$ be a triangle with incentre $I$ and inradius $r$ . Let $D, E, F$ be the feet of the perpendiculars from $I$ to the sides $B C, C A$ and $A B$ , respectively. If $r_{1}, r_{2}$ and $r_{3}$ are the radii of circles inscribed in the quadrilaterals $A F I E, B D I F$ and CEID respectively, then prove that

$\frac{r_{1}}{r - r_{1}} + \frac{r_{2}}{r - r_{2}} + \frac{r_{3}}{r - r_{3}} = \frac{r_{1} r_{2} r_{3}}{(r - r_{1}) (r - r_{2}) (r - r_{3})}$ .

(2000 3M)

Show Answer

Solution:

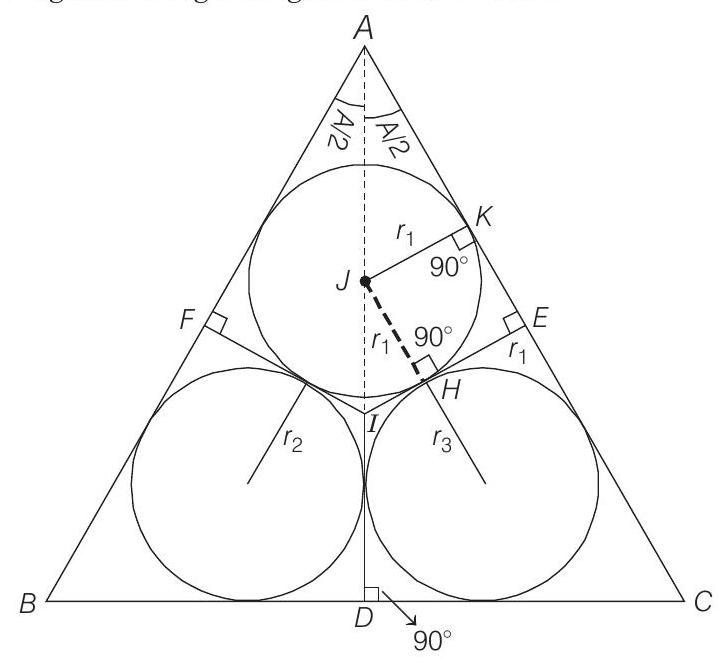
The quadrilateral $H E K J$ is a square, because all four angles are right angles and $J K = J H$ .

Therefore, $H E = J K = r_{1}$ and $I E = r$ [given]

$\Rightarrow I H = r - r_{1}$

Now, in right angled $△ I H J$ ,

$∠ J I H = π / 2 - A / 2$

$[∵ ∠ I E A = 90^{\circ}, ∠ I A E = A / 2$ and $∠ J I H = ∠ A I E]$

In $△ J I H$ ,

$\tan \frac{π}{2} - \frac{A}{2} = \frac{r_{1}}{r - r_{1}} \Rightarrow \cot \frac{A}{2} = \frac{r_{1}}{r - r_{1}}$

Similarly, $\cot \frac{B}{2} = \frac{r_{2}}{r - r_{2}}$ and $\cot \frac{C}{2} = \frac{r_{3}}{r - r_{3}}$

On adding above results, we get $\cot A / 2 + \cot B / 2 + \cot C / 2$

$= \cot A / 2 \cot B / 2 \cot C / 2$

$\Rightarrow \frac{r_{1}}{r - r_{1}} + \frac{r_{2}}{r - r_{2}} + \frac{r_{3}}{r - r_{3}} = \frac{r_{1} r_{2} r_{3}}{(r - r_{1}) (r - r_{2}) (r - r_{3})}$

Properties of Triangles 3 Question 17

Solution:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Properties of Triangles 3 Question 17

17. Let ABC be a triangle with incentre I and inradius r. Let D,E,F be the feet of the perpendiculars from I to the sides BC,CA and AB, respectively. If r1,r2 and r3 are the radii of circles inscribed in the quadrilaterals AFIE,BDIF and CEID respectively, then prove that

Solution:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu