Properties of Triangles 3 Question 17
17. Let
(2000 3M)
Show Answer
Solution:
- The quadrilateral
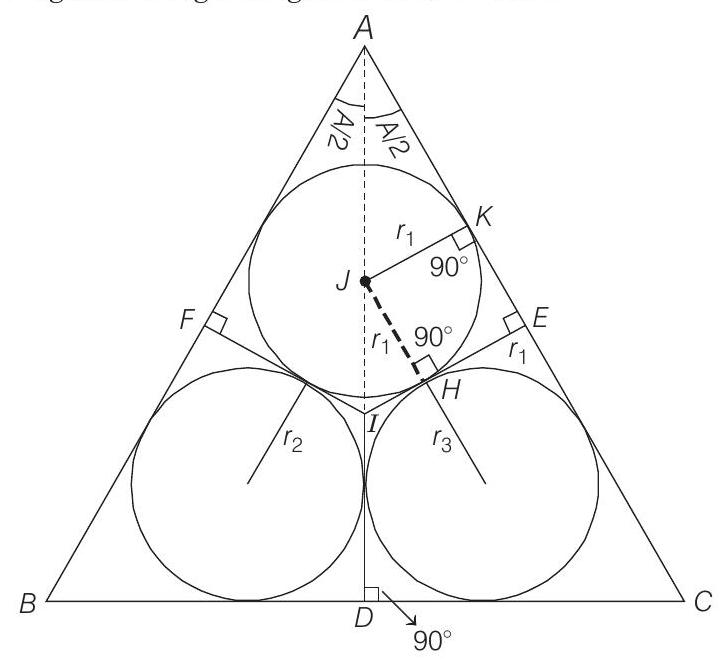
Therefore,
Now, in right angled
In
Similarly,
On adding above results, we get






