Permutations and Combinations 2 Question 24
24. $m n$ squares of equal size are arranged to form a rectangle of dimension $m$ by $n$ where $m$ and $n$ are natural numbers. Two squares will be called ’neighbours’ if they have exactly one common side. A natural number is written in each square such that the number in written any square is the arithmetic mean of the numbers written in its neighbouring squares. Show that this is possible only if all the numbers used are equal.
(1982, 5M)
Show Answer
Solution:
- Let $m n$ squares of equal size are arrange to form a rectangle of dimension $m$ by $n$. Shown as, from figure.
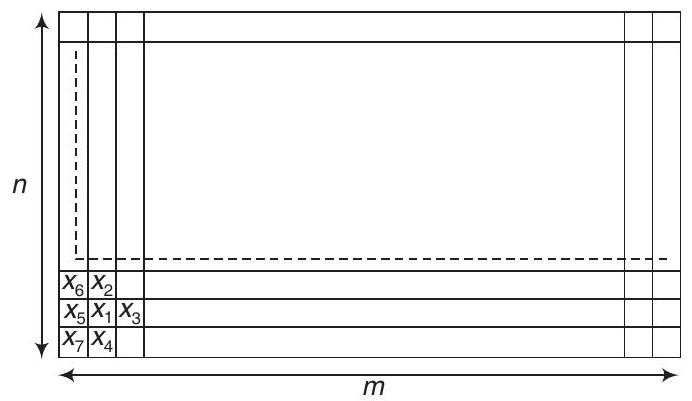
neighbours of $x _1$ are ${x _2, x _3, x _4, x _5 } x _5$ are ${x _1, x _6, x _7 }$ and $x _7$ are ${x _5, x _4 }$.
$$ \begin{array}{ll} \Rightarrow \quad & x _1=\frac{x _2+x _3+x _4+x _5}{4}, \quad x _5=\frac{x _1+x _6+x _7}{3} \\ \text { and } \quad x _7=\frac{x _4+x _5}{2} \\ \therefore \quad 4 x _1=x _2+x _3+x _4+\frac{x _1+x _6+x _7}{3} \\ \Rightarrow \quad 12 x _1=3 x _2+3 x _3+3 x _4+x _1+x _6+\frac{x _4+x _5}{2} \\ \Rightarrow \quad 24 x _1=6 x _2+6 x _3+6 x _4+2 x _1+2 x _6+x _4+x _5 \\ \Rightarrow \quad 22 x _1=6 x _2+6 x _3+7 x _4+x _5+2 x _6 \end{array} $$
where, $x _1, x _2, x _3, x _4, x _5, x _6$ are all the natural numbers and $x _1$ is linearly expressed as the sum of $x _2, x _3, x _4, x _5, x _6$ where sum of coefficients are equal only if, all observations are same.
$$ \Rightarrow \quad x _2=x _3=x _4=x _5=x _6 $$
$\Rightarrow$ All the numbers used are equal
