SATHEE: Parabola 3 Question 8

Parabola 3 Question 8

8. If the normals of the parabola $y^{2} = 4 x$ drawn at the end points of its latusrectum are tangents to the circle $(x - 3)^{2} + (y + 2)^{2} = r^{2}$ , then the value of $r^{2}$ is

(2015 Adv.)

Analytical & Descriptive Questions

Show Answer

Answer:

Correct Answer: 8. (2)

Solution:

Equation of any tangent to the parabola, $y^{2} = 4 a x$ is $y = m x + \frac{a}{m}$ .

This line will touch the circle $x^{2} + y^{2} = \frac{a^{2}}{2}$

$\begin{array}{cc} If & {\frac{a}{m}}^{2} = \frac{a^{2}}{2} (m^{2} + 1) \\ \Rightarrow & \frac{1}{m^{2}} = \frac{1}{2} (m^{2} + 1) \\ \Rightarrow & 2 = m^{4} + m^{2} \\ \Rightarrow & m^{4} + m^{2} - 2 = 0 \\ \Rightarrow & (m^{2} - 1) (m^{2} + 2) = 0 \\ \Rightarrow & m^{2} - 1 = 0, m^{2} = - 2 \\ \Rightarrow & m = \pm 1 [m^{2} = - 2 is not possible] \end{array}$

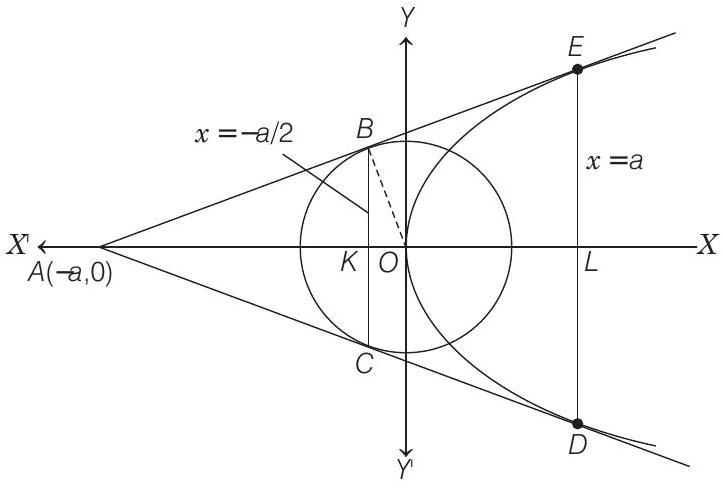
Therefore, two common tangents are

$y = x + a and y = - x - a$

These two intersect at $A (- a, 0)$ .

The chord of contact of $A (- a, 0)$ for the circle

$x^{2} + y^{2} = a^{2} / 2 is (- a) x + 0 \cdot y = a^{2} / 2$

$\Rightarrow x = - a / 2$

and chord of contact of $A (- a, 0)$ for the parabola $y^{2} = 4 a x$ is $0 \cdot y = 2 a (x - a) \Rightarrow x = a$

Again, length of $B C = 2 B K$

$\begin{aligned} = 2 \sqrt{O B^{2} - O K^{2}} \\ = 2 \sqrt{\frac{a^{2}}{2} - \frac{a^{2}}{4}} = 2 \sqrt{\frac{a^{2}}{4}} = a \end{aligned}$

and we know that, $D E$ is the latusrectum of the parabola, so its length is $4 a$ .

Thus, area of the quadrilateral $B C D E$

$\begin{aligned} = \frac{1}{2} (B C + D E) (K L) \\ = & \frac{1}{2} (a + 4 a) \frac{3 a}{2} = \frac{15 a^{2}}{4} \end{aligned}$

Parabola 3 Question 8

8. If the normals of the parabola $y^{2} = 4 x$ drawn at the end points of its latusrectum are tangents to the circle $(x - 3)^{2} + (y + 2)^{2} = r^{2}$ , then the value of $r^{2}$ is

Analytical & Descriptive Questions

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Parabola 3 Question 8

8. If the normals of the parabola y2=4x drawn at the end points of its latusrectum are tangents to the circle (x−3)2+(y+2)2=r2, then the value of r2 is

Analytical & Descriptive Questions

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu

8. If the normals of the parabola $y^{2} = 4 x$ drawn at the end points of its latusrectum are tangents to the circle $(x - 3)^{2} + (y + 2)^{2} = r^{2}$ , then the value of $r^{2}$ is