Parabola 3 Question 8
8. If the normals of the parabola $y^{2}=4 x$ drawn at the end points of its latusrectum are tangents to the circle $(x-3)^{2}+(y+2)^{2}=r^{2}$, then the value of $r^{2}$ is
(2015 Adv.)
Analytical & Descriptive Questions
Show Answer
Answer:
Correct Answer: 8. (2)
Solution:
- Equation of any tangent to the parabola, $y^{2}=4 a x$ is $y=m x+\frac{a}{m}$.
This line will touch the circle $x^{2}+y^{2}=\frac{a^{2}}{2}$
$$ \begin{array}{cc} \text { If } & \frac{a}{m}^{2}=\frac{a^{2}}{2}\left(m^{2}+1\right) \\ \Rightarrow & \frac{1}{m^{2}}=\frac{1}{2}\left(m^{2}+1\right) \\ \Rightarrow & 2=m^{4}+m^{2} \\ \Rightarrow & m^{4}+m^{2}-2=0 \\ \Rightarrow & \left(m^{2}-1\right)\left(m^{2}+2\right)=0 \\ \Rightarrow & m^{2}-1=0, m^{2}=-2 \\ \Rightarrow & m= \pm 1 \quad\left[m^{2}=-2 \text { is not possible }\right] \end{array} $$
Therefore, two common tangents are
$$ y=x+a \quad \text { and } \quad y=-x-a $$
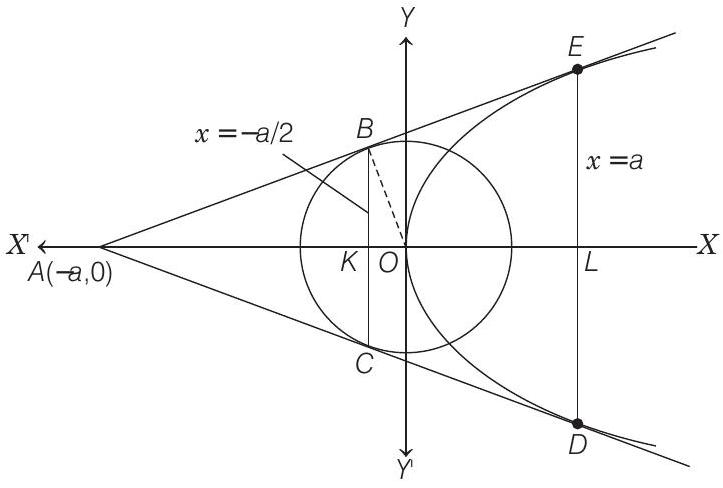
These two intersect at $A(-a, 0)$.
The chord of contact of $A(-a, 0)$ for the circle
$$ x^{2}+y^{2}=a^{2} / 2 \text { is }(-a) x+0 \cdot y=a^{2} / 2 $$
$$ \Rightarrow \quad x=-a / 2 $$
and chord of contact of $A(-a, 0)$ for the parabola $y^{2}=4 a x$ is $0 \cdot y=2 a(x-a) \quad \Rightarrow \quad x=a$
Again, length of $B C=2 B K$
$$ \begin{aligned} & =2 \sqrt{O B^{2}-O K^{2}} \\ & =2 \sqrt{\frac{a^{2}}{2}-\frac{a^{2}}{4}}=2 \sqrt{\frac{a^{2}}{4}}=a \end{aligned} $$
and we know that, $D E$ is the latusrectum of the parabola, so its length is $4 a$.
Thus, area of the quadrilateral $B C D E$
$$ \begin{aligned} & =\frac{1}{2}(B C+D E)(K L) \\ = & \frac{1}{2}(a+4 a) \quad \frac{3 a}{2}=\frac{15 a^{2}}{4} \end{aligned} $$






