SATHEE: Parabola 3 Question 5

Parabola 3 Question 5

5. A solution curve of the differential equation $(x^{2} + x y + 4 x + 2 y + 4) \frac{d y}{d x} - y^{2} = 0, x > 0,$ passes through the point $(1, 3)$ . Then, the solution curve

(a) intersects $y = x + 2$ exactly at one point

(2016 Adv.)

(b) intersects $y = x + 2$ exactly at two points

(d) does not intersect $y = (x + 3)^{2}$

Show Answer

Answer:

Correct Answer: 5. (a, d)

Solution:

Since, $R - a, a t - \frac{1}{t}$ lies on $y = 2 x + a$ .

$\Rightarrow a \cdot t - \frac{1}{t} = - 2 a + a \Rightarrow t - \frac{1}{t} = - 1$

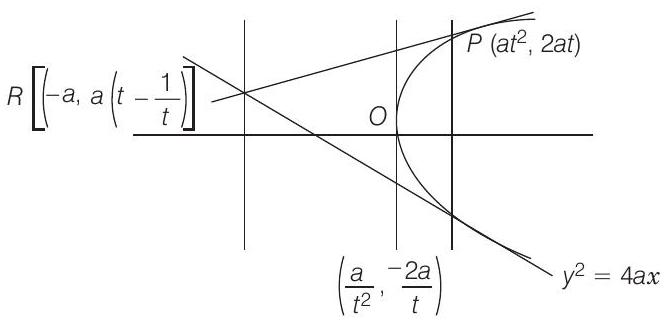
Thus, length of focal chord

$= a t + {\frac{1}{t}}^{2} = a t - {\frac{1}{t}}^{2} + 4 = 5 a$

Play Store

App Store

Ask SATHEE

Welcome to SATHEE !
Select from 'Menu' to explore our services, or ask SATHEE to get started. Let's embark on this journey of growth together! 🌐📚🚀🎓

I'm relatively new and can sometimes make mistakes.
If you notice any error, such as an incorrect solution, please use the thumbs down icon to aid my learning.
To begin your journey now, click on "I understand".

Parabola 3 Question 5

5. A solution curve of the differential equation (x2+xy+4x+2y+4)dydx−y2=0,x>0, passes through the point (1,3). Then, the solution curve

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu

5. A solution curve of the differential equation $(x^{2} + x y + 4 x + 2 y + 4) \frac{d y}{d x} - y^{2} = 0, x > 0,$ passes through the point $(1, 3)$ . Then, the solution curve