Parabola 3 Question 5
5. A solution curve of the differential equation $\left(x^{2}+x y+4 x+2 y+4\right) \frac{d y}{d x}-y^{2}=0, \quad x>0, \quad$ passes through the point $(1,3)$. Then, the solution curve
(a) intersects $y=x+2$ exactly at one point
(2016 Adv.)
(b) intersects $y=x+2$ exactly at two points
(c) intersects $y=(x+2)^{2}$
(d) does not intersect $y=(x+3)^{2}$
Show Answer
Answer:
Correct Answer: 5. (a, d)
Solution:
- Since, $R-a, a \quad t-\frac{1}{t} \quad$ lies on $y=2 x+a$.
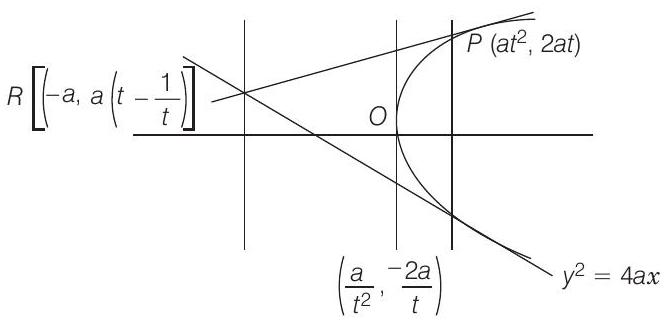$\Rightarrow \quad a \cdot t-\frac{1}{t}=-2 a+a \Rightarrow \quad t-\frac{1}{t}=-1$
Thus, length of focal chord
$$ =a \quad t+\frac{1}{t}^{2}=a \quad t-\frac{1}{t}^{2}+4=5 a $$
