Limit Continuity and Differentiability 5 Question 1
1. Let
(a) 18
(b) 24
(c) 12
(d) 36
Show Answer
Answer:
Correct Answer: 1. (a)
Solution:
- Given,
Now,
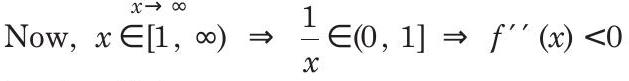
Option (d) is correct.
As
So, graph of
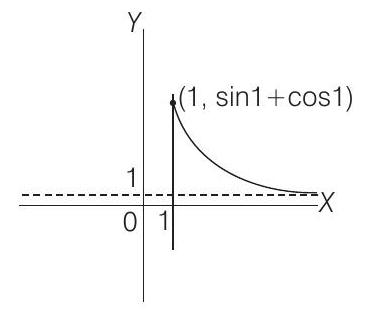
Now, in
As,
For all
For all






