Limit Continuity and Differentiability 5 Question 1
1. Let $f: R \rightarrow R$ be a continuously differentiable function such that $f(2)=6$ and $f^{\prime}(2)=\frac{1}{48}$. If $\int _6^{f(x)} 4 t^{3} d t=(x-2) g(x)$, then $\lim _{x \rightarrow 2} g(x)$ is equal to (2019 Main, 12 April I)
(a) 18
(b) 24
(c) 12
(d) 36
$$ \frac{\sin (p+1) x+\sin x}{x}, x<0 $$
Show Answer
Answer:
Correct Answer: 1. (a)
Solution:
- Given, $f(x)=x \cos \frac{1}{x}, x \geq 1 \Rightarrow f^{\prime}(x)=\frac{1}{x} \sin \frac{1}{x}+\cos \frac{1}{x}$
$\Rightarrow \quad f^{\prime \prime}(x)=-\frac{1}{x^{3}} \cos \frac{1}{x}$
Now, $\quad \lim _{x \rightarrow \infty} f^{\prime}(x)=0+1=1 \Rightarrow$ Option (b) is correct.
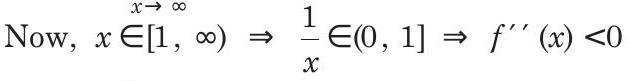
Option (d) is correct.
As $f^{\prime}(1)=\sin 1+\cos 1>1$
$f^{\prime}(x)$ is strictly decreasing and $\lim _{x \rightarrow \infty} f^{\prime}(x)=1$
So, graph of $f^{\prime}(x)$ is shown as below.
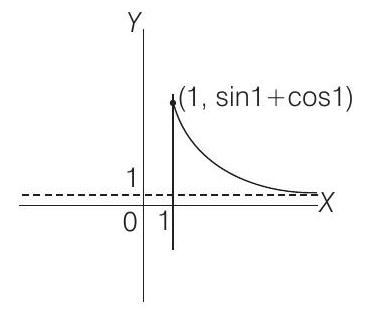
Now, in $[x, x+2], x \in[1, \infty), f(x)$ is continuous and differentiable so by LMVT,
$f^{\prime}(x)=\frac{f(x+2)-f(x)}{2}$
As, $\quad f^{\prime}(x)>1$
For all $x \in[1, \infty)$
$\Rightarrow \quad \frac{f(x+2)-f(x)}{2}>1 \Rightarrow f(x+2)-f(x)>2$
For all $x \in[1, \infty)$
