Inverse Circular Functions 2 Question 9
9. Match List I with List II and select the correct answer using the code given below the lists.
| List I | List II | ||
|---|---|---|---|
| P. $\frac{1}{y^{2}} \frac{\cos \left(\tan ^{-1} y\right)+y \sin \left(\tan ^{-1} y\right)^{2}}{\cot \left(\sin ^{-1} y\right)+\tan \left(\sin ^{-1} y\right)}+y^{4} \quad$ takes value | 1. | $\frac{1}{2} \sqrt{\frac{5}{3}}$ | |
| Q. If $\cos x+\cos y+\cos z=0=\sin x+\sin y+\sin z$, then | 2. | $\sqrt{2}$ | |
| possible value of $\cos \frac{x-y}{2}$ is | |||
| R. If $\cos \frac{\pi}{4}-x \cos 2 x+\sin x \sin 2 x \sec x$ | |||
| $=\cos x \sin 2 x \sec x+\cos \frac{\pi}{4}+x \cos 2 x$, then | |||
| possible value of $\sec x$ is | |||
| S. If $\cot \left(\sin ^{-1} \sqrt{1-x^{2}}\right)=\sin \left[\tan ^{-1}(x \sqrt{6})\right]$, | |||
| $x=0$. Then, possible value of $x$ is |
Codes
| P | Q | R | S | |
|---|---|---|---|---|
| (a) | 4 | 3 | 1 | 2 |
| (b) | 4 | 3 | 2 | 1 |
| (c) | 3 | 4 | 2 | 1 |
| (d) | 3 | 4 | 1 | 2 |
Show Answer
Answer:
Correct Answer: 9. $P \rightarrow 4 ; Q \rightarrow 3 ; R \rightarrow 2 ; S \rightarrow 1$
Solution:
- P. Here, innermost function is inverse.
$\therefore$ Put $\tan ^{-1} y=\theta \Rightarrow \tan \theta=y$
$ \frac{1}{y^{2}} \cdot \frac{\cos \left(\tan ^{-1} y\right)+y \sin \left(\tan ^{-1} y\right)}{\cot \left(\sin ^{-1} y\right)+\tan \left(\sin ^{-1} y\right)}+y^{4} $
$=\frac{1}{y^{2}} \frac{\frac{1}{\sqrt{1+y^{2}}}+\frac{y^{2}}{\sqrt{1+y^{2}}}}{\frac{\sqrt{1-y^{2}}}{y}+\frac{y}{\sqrt{1-y^{2}}}}+y^{4}$
$=\frac{1}{y^{2}} \cdot y^{2}\left(1-y^{4}\right)+y^{4}{ }^{1 / 2}=1$
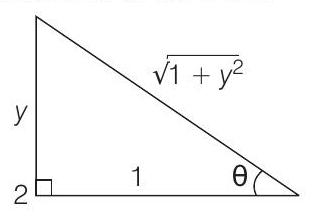
Q. Given,
$\cos x+\cos y=-\cos z$
and
$\sin x+\sin y=-\sin z$
On squaring and adding, we get
$\cos ^{2} x+\sin ^{2} x+\cos ^{2} y+\sin ^{2} y+2 \cos x \cos y$
$+2 \sin x \sin y=1$
$\Rightarrow \quad 2+2[\cos (x-y)]=1 \quad \Rightarrow \quad \cos (x-y)=-\frac{1}{2}$
$\Rightarrow 2 \cos ^{2} \frac{x-y}{2}-1=-\frac{1}{2}$
$\Rightarrow \quad 2 \cos ^{2} \frac{x-y}{2}=\frac{1}{2}$
$\Rightarrow \quad \cos \frac{x-y}{2}=\frac{1}{2}$
R. $\cos 2 x \cdot \cos \frac{\pi}{4}-x-\cos \frac{\pi}{4}+x+2 \sin ^{2} x$
$=2 \sin x \cdot \cos x$
$\Rightarrow \quad \cos 2 x \cdot(\sqrt{2} \sin x)+2 \sin ^{2} x=2 \sin x \cdot \cos x$
$\Rightarrow \quad \sqrt{2} \sin x[\cos 2 x+\sqrt{2} \sin x-\sqrt{2} \cos x]=0$
$\Rightarrow \quad \sin x=0,(\cos x-\sin x)(\cos x+\sin x-\sqrt{2})=0$
$\Rightarrow \quad \sec x=1$ or $\tan x=1$
$\Rightarrow \quad \sec x=1$ or $\sqrt{2}$
S. $\cot \left(\sin ^{-1} \sqrt{1-x^{2}}\right)=\sin \left(\tan ^{-1}(x \sqrt{6})\right)$
$ \begin{aligned} & \Rightarrow \quad \frac{x}{\sqrt{1-x^{2}}}=\frac{x \sqrt{6}}{\sqrt{1+6 x^{2}}} \\ & \Rightarrow \quad 1+6 x^{2}=6-6 x^{2} \\ & \Rightarrow \quad 12 x^{2}=5 \quad \Rightarrow \quad x=\sqrt{\frac{5}{12}}=\frac{\sqrt{5}}{2 \sqrt{3}} \end{aligned} $
$(P) \rightarrow 4,(Q) \rightarrow 3,(R) \rightarrow 2$ or $4,(S) \rightarrow 1$
