Inverse Circular Functions 2 Question 15
15. If
(2014 Adv.)
Show Answer
Solution:
- PLAN
(i) Using definition of
(ii) The number of solutions of equations involving trigonometric and algebraic functions and involving both functions are found using graphs of the curves.
We know that,
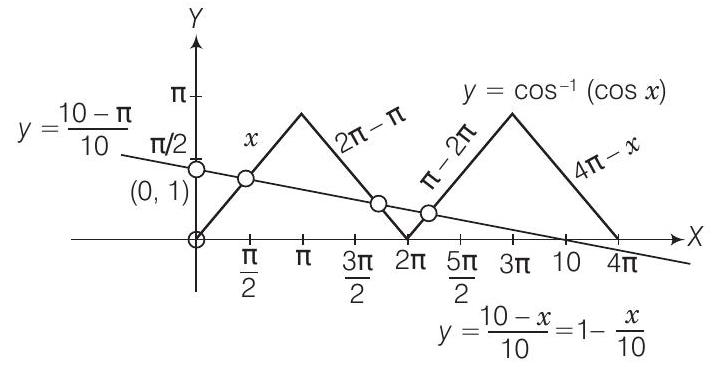
From above graph, it is clear that






