SATHEE: Hyperbola 1 Question 16

Hyperbola 1 Question 16

17.

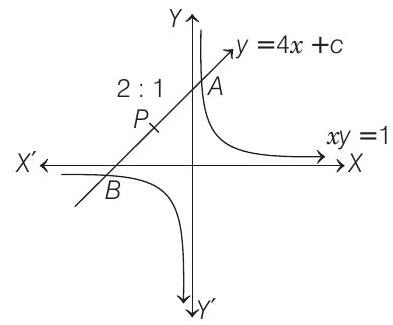
A variable straight line of slope 4 intersects the hyperbola $x y = 1$ at two points. Find the locus of the point which divides the line segment between these two points in the ratio $1 : 2$ .

(1997, 5M)

Show Answer

Answer:

Correct Answer: 17. ( $16 x^{2} + y^{2} + 10 x y = 2$ )

Solution:

Let $y = 4 x + c$ meets $x y = 1$ at two points $A$ and $B$ .

i.e. $A (t_{1}, 1 / t_{1}), B (t_{2}, 1 / t_{2})$ $∴$

Coordinates of $P$ are

$\frac{2 t_{1} + t_{2}}{2 + 1}, \frac{2 \cdot \frac{1}{t_{1}} + 1 \cdot \frac{1}{t_{2}}}{2 + 1} = (h, k)$

$∴ h = \frac{2 t_{1} + t_{2}}{3}$ and $k = \frac{2 t_{2} + t_{1}}{3 t_{1} t_{2}}$

Also, $t_{1}, \frac{1}{t_{1}}$ and $t_{2}, \frac{1}{t_{2}}$ lie on $y = 4 x + c$ .

$\Rightarrow \frac{\frac{1}{t_{2}} - \frac{1}{t_{1}}}{t_{2} - t_{1}} = \frac{1}{t_{1} t_{2}} = 4$ or $t_{1} t_{2} = - 1 / 4$

From Eq. (i), $t_{1} = 2 h + \frac{k}{4}$

$and t_{1} = h - \frac{k}{2}$

From Eqs. (ii) and (iii), $- h - \frac{k}{2} 2 h + \frac{k}{4} = - \frac{1}{4}$

$\begin{array}{lll} \Rightarrow & - \frac{2 h + k}{2} \frac{8 h + k}{4} = - \frac{1}{4} \\ \Rightarrow & (2 h + k) (8 h + k) = 2 \\ \Rightarrow & 16 h^{2} + k^{2} + 10 h k = 2 \end{array}$

Hence, required locus is $16 x^{2} + y^{2} + 10 x y = 2$ .

Hyperbola 1 Question 16

17.

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Hyperbola 1 Question 16

17.

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu