Functions 3 Question 4
4. If $f:[1, \infty) \rightarrow[2, \infty)$ is given by $f(x)=x+\frac{1}{x}$, then $f^{-1}(x)$ equals
(2001, 1M)
(a) $\frac{x+\sqrt{x^{2}-4}}{2}$
(b) $\frac{x}{1+x^{2}}$
(c) $\frac{x-\sqrt{x^{2}-4}}{2}$
(d) $1+\sqrt{x^{2}-4}$
Show Answer
Answer:
Correct Answer: 4. (a)
Solution:
- We have, $f(x)=\frac{x}{1+x^{2}}, x \in R$
Ist Method $f(x)$ is an odd function and maximum occur at $x=1$
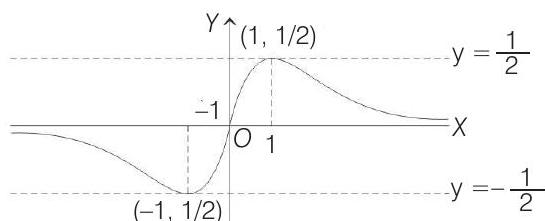
From the graph it is clear that range of $f(x)$ is
$$ -\frac{1}{2}, \frac{1}{2} $$
IInd Method $f(x)=\frac{1}{x+\frac{1}{x}}$
If $x>0$, then by AM $\geq GM$, we get $x+\frac{1}{x} \geq 2$
$$ \Rightarrow \quad \frac{1}{x+\frac{1}{x}} \leq \frac{1}{2} \quad \Rightarrow \quad 0<f(x) \leq \frac{1}{2} $$
If $x<0$, then by AM $\geq$ GM, we get $x+\frac{1}{x} \leq-2$
$$ \Rightarrow \quad \frac{1}{x+\frac{1}{x}} \geq-\frac{1}{2} \quad \Rightarrow-\frac{1}{2} \leq f(x)<0 $$
If $x=0$, then $f(x)=\frac{0}{1+0}=0$
Thus,
$$ -\frac{1}{2} \leq f(x) \leq \frac{1}{2} $$
Hence, $f(x) \in-\frac{1}{2}, \frac{1}{2}$
IIIrd Method
Let $y=\frac{x}{1+x^{2}} \Rightarrow y x^{2}-x+y=0$
$\because x \in R$, so $D \geq 0$
$\Rightarrow \quad 1-4 y^{2} \geq 0$ $\Rightarrow(1-2 y)(1+2 y) \geq 0 \Rightarrow y \in-\frac{1}{2}, \frac{1}{2}$
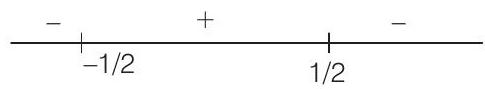
So, range is $-\frac{1}{2}, \frac{1}{2}$.
