Functions 3 Question 4
4. If
(2001, 1M)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 4. (a)
Solution:
- We have,
Ist Method
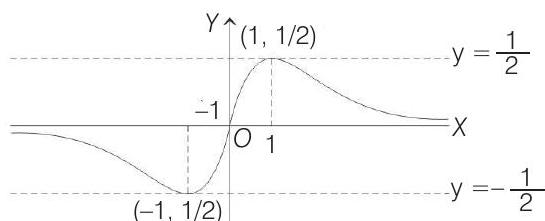
From the graph it is clear that range of
IInd Method
If
If
If
Thus,
Hence,
IIIrd Method
Let
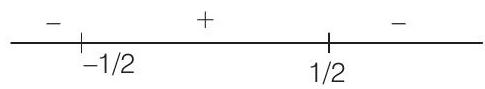
So, range is






