Ellipse 2 Question 9
9. The area (in sq units) of the quadrilateral formed by the tangents at the end points of the latusrectum to the ellipse $\frac{x^{2}}{9}+\frac{y^{2}}{5}=1$ is
(2015 Main)
(a) $\frac{27}{4}$
(b) 18
(c) $\frac{27}{2}$
(d) 27
Show Answer
Answer:
Correct Answer: 9. (d)
Solution:
- Given equation of ellipse is
$ \begin{array}{lc} & \frac{x^{2}}{9}+\frac{y^{2}}{5}=1 \\ \therefore & a^{2}=9, b^{2}=5 \Rightarrow a=3, b=\sqrt{5} \\ \text { Now, } & e=\sqrt{1+\frac{b^{2}}{a^{2}}}=\sqrt{1-\frac{5}{9}}=\frac{2}{3} \end{array} $
Foci $=( \pm a e, 0)=( \pm 2,0)$ and $\frac{b^{2}}{a}=\frac{5}{3}$
$\therefore$ Extremities of one of latusrectum are
$ 2, \frac{5}{3} \text { and } 2, \frac{-5}{3} $
$\therefore$ Equation of tangent at $2, \frac{5}{3}$ is
$ \frac{x(2)}{9}+\frac{y(5 / 3)}{5}=1 \quad \text { or } \quad 2 x+3 y=9 $
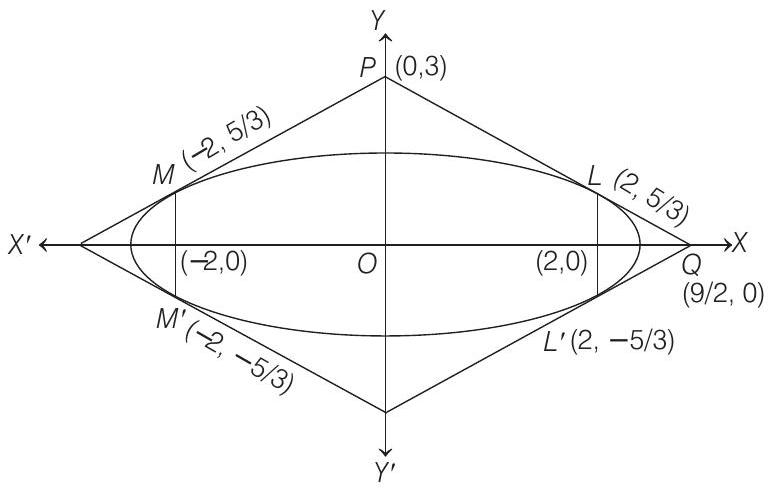
Since, Eq. (ii) intersects $X$ and $Y$-axes at $\frac{9}{2}, 0$ and $(0,3)$, respectively.
$\therefore$ Area of quadrilateral $=4 \times$ Area of $\triangle P O Q$
$ =4 \times \frac{1}{2} \times \frac{9}{2} \times 3=27 \text { sq units } $
