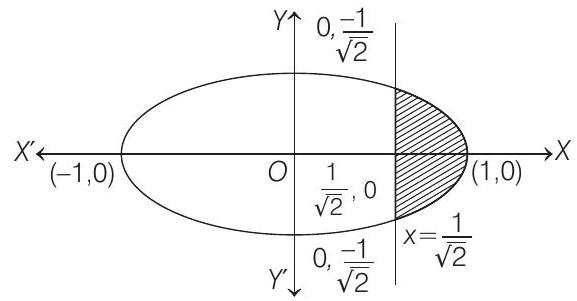
Ellipse 1 Question 7
8. Consider two straight lines, each of which is tangent to both the circle $x^{2}+y^{2}=(1 / 2)$ and the parabola $y^{2}=4 x$. Let these lines intersect at the point $Q$. Consider the ellipse whose centre is at the origin $O(0,0)$ and whose semi-major axis is $O Q$. If the length of the minor axis of this ellipse is $\sqrt{2}$, then which of the following statement(s) is (are) TRUE?
(2018 Adv.)
(a) For the ellipse, the eccentricity is $1 / \sqrt{2}$ and the length of the latus rectum is 1
(b) For the ellipse, the eccentricity is $1 / 2$ and the length of the latus rectum is $1 / 2$
(c) The area of the region bounded by the ellipse between the lines $x=\frac{1}{\sqrt{2}}$ and $x=1$ is $\frac{1}{4 \sqrt{2}}(\pi-2)$
(d) The area of the region bounded by the ellipse between the lines $x=\frac{1}{\sqrt{2}}$ and $x=1$ is $\frac{1}{16}(\pi-2)$
Fill in the Blanks
Show Answer
Answer:
Correct Answer: 8. $(a, c)$
Solution:
- We have,
Equation of circle $x^{2}+y^{2}=\frac{1}{2}$
and Equation of parabola $y^{2}=4 x$
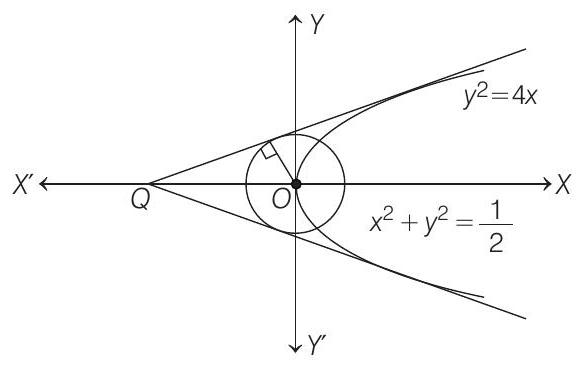
Let the equation of common tangent of parabola and circle is
$ y=m x+\frac{1}{m} $
Since, radius of circle $=\frac{1}{\sqrt{2}}$
$ \begin{array}{ll} \therefore & \frac{1}{\sqrt{2}}=\left|\frac{0+0+\frac{1}{m}}{\sqrt{1+m^{2}}}\right| \\ \Rightarrow & m^{4}+m^{2}-2=0 \Rightarrow m= \pm 1 \end{array} $
$\therefore$ Equation of common tangents are
$ y=x+1 \text { and } y=-x-1 $
Intesection point of common tangent at $Q(-1,0)$
$\therefore$ Equation of ellipse $\frac{x^{2}}{1}+\frac{y^{2}}{1 / 2}=1$
where, $a^{2}=1, b^{2}=1 / 2$
Now, eccentricity $(e)=\sqrt{1-\frac{b^{2}}{a^{2}}}=\sqrt{1-\frac{1}{2}}=\frac{1}{\sqrt{2}}$
and length of latusrectum $=\frac{2 b^{2}}{a}=\frac{2 \frac{1}{2}}{1}=1$
$\therefore$ Area of shaded region
$ \begin{gathered} =2 \int _{1 / \sqrt{2}}^{1} \frac{1}{\sqrt{2}} \sqrt{1-x^{2}} d x \\ =\sqrt{2} \frac{x}{2} \sqrt{1-x^{2}}+\frac{1}{2} \sin ^{-1} x _{1 / \sqrt{2}}^{1} \\ =\sqrt{2} \quad 0+\frac{\pi}{4}-\frac{1}{4}+\frac{\pi}{8} \\ =\sqrt{2} \frac{\pi}{8}-\frac{1}{4}=\frac{\pi-2}{4 \sqrt{2}} \end{gathered} $
