SATHEE: Ellipse 1 Question 7

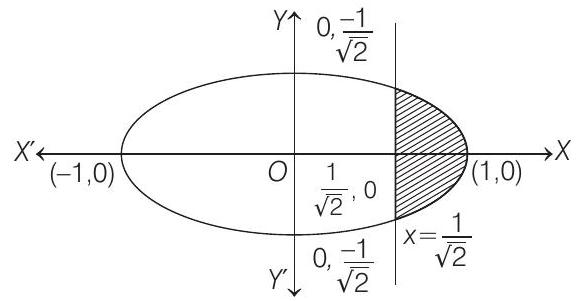
Ellipse 1 Question 7

8. Consider two straight lines, each of which is tangent to both the circle $x^{2} + y^{2} = (1 / 2)$ and the parabola $y^{2} = 4 x$ . Let these lines intersect at the point $Q$ . Consider the ellipse whose centre is at the origin $O (0, 0)$ and whose semi-major axis is $O Q$ . If the length of the minor axis of this ellipse is $\sqrt{2}$ , then which of the following statement(s) is (are) TRUE?

(2018 Adv.)

(a) For the ellipse, the eccentricity is $1 / \sqrt{2}$ and the length of the latus rectum is 1

(b) For the ellipse, the eccentricity is $1 / 2$ and the length of the latus rectum is $1 / 2$

(c) The area of the region bounded by the ellipse between the lines $x = \frac{1}{\sqrt{2}}$ and $x = 1$ is $\frac{1}{4 \sqrt{2}} (π - 2)$

(d) The area of the region bounded by the ellipse between the lines $x = \frac{1}{\sqrt{2}}$ and $x = 1$ is $\frac{1}{16} (π - 2)$

Fill in the Blanks

Show Answer

Answer:

Correct Answer: 8. $(a, c)$

Solution:

We have,

Equation of circle $x^{2} + y^{2} = \frac{1}{2}$

and Equation of parabola $y^{2} = 4 x$

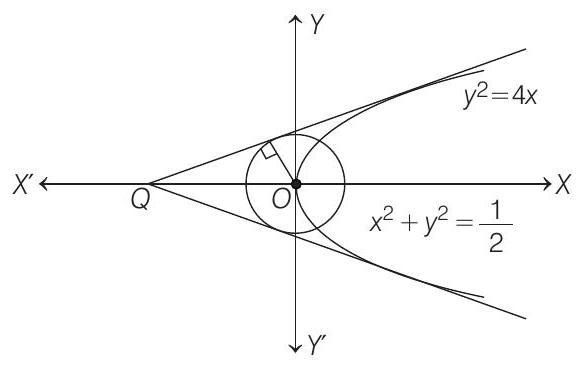
Let the equation of common tangent of parabola and circle is

$y = m x + \frac{1}{m}$

Since, radius of circle $= \frac{1}{\sqrt{2}}$

$\begin{array}{ll} ∴ & \frac{1}{\sqrt{2}} = | \frac{0 + 0 + \frac{1}{m}}{\sqrt{1 + m^{2}}} | \\ \Rightarrow & m^{4} + m^{2} - 2 = 0 \Rightarrow m = \pm 1 \end{array}$

$∴$ Equation of common tangents are

$y = x + 1 and y = - x - 1$

Intesection point of common tangent at $Q (- 1, 0)$

$∴$ Equation of ellipse $\frac{x^{2}}{1} + \frac{y^{2}}{1 / 2} = 1$

where, $a^{2} = 1, b^{2} = 1 / 2$

Now, eccentricity $(e) = \sqrt{1 - \frac{b^{2}}{a^{2}}} = \sqrt{1 - \frac{1}{2}} = \frac{1}{\sqrt{2}}$

and length of latusrectum $= \frac{2 b^{2}}{a} = \frac{2 \frac{1}{2}}{1} = 1$

$∴$ Area of shaded region

$\begin{matrix} = 2 \int_{1 / \sqrt{2}}^{1} \frac{1}{\sqrt{2}} \sqrt{1 - x^{2}} d x \\ = \sqrt{2} \frac{x}{2} \sqrt{1 - x^{2}} + \frac{1}{2} \sin^{- 1} x_{1 / \sqrt{2}}^{1} \\ = \sqrt{2} 0 + \frac{π}{4} - \frac{1}{4} + \frac{π}{8} \\ = \sqrt{2} \frac{π}{8} - \frac{1}{4} = \frac{π - 2}{4 \sqrt{2}} \end{matrix}$