Ellipse 1 Question 10
11. Let
(1994, 2M)
Analytical & Descriptive Question
Show Answer
Answer:
Correct Answer: 11.
Solution:
- Given,
Foci
The area
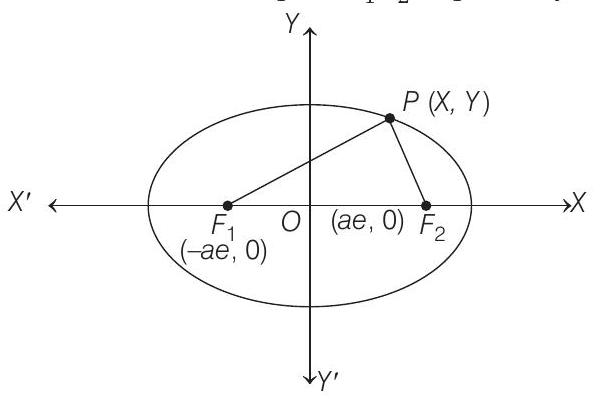
So,






