Differential Equations 1 Question 18
18. Let $y=f(x)$ be a curve passing through $(1,1)$ such that the triangle formed by the coordinate axes and the tangent at any point of the curve lies in the first quadrant and has area 2 unit. Form the differential equation and determine all such possible curves.
$(1995,5$ M)
Integer Answer Type Question
Show Answer
Answer:
Correct Answer: 18. (b)
Solution:
- Equation of tangent to the curve $y=f(x)$ at point
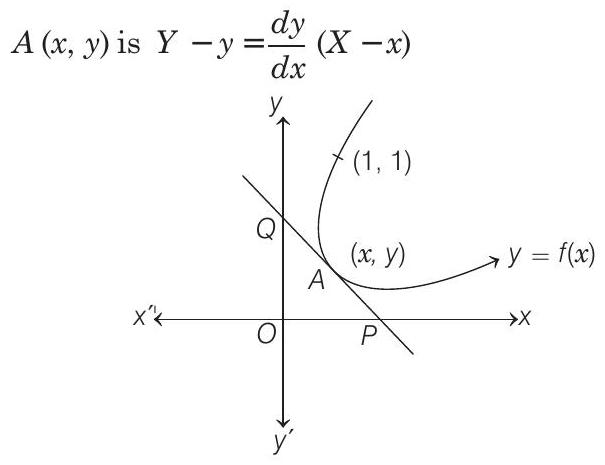
whose, $x$-intercept $x-y \cdot \frac{d x}{d y}, 0$
$$ y \text {-intercept } 0, y-x \frac{d y}{d x} $$
Given, $\quad \triangle O P Q=2$
$\Rightarrow \quad \frac{1}{2} \cdot x-y \frac{d x}{d y} \quad y-x \frac{d y}{d x}=2$
$$ \Rightarrow \quad x-y \frac{1}{p}(y-x p)=4, \text { where } \quad p=\frac{d y}{d x} $$
$\Rightarrow \quad p^{2} x^{2}-2 p x y+4 p+y^{2}=0$
$\Rightarrow \quad(y-p x)^{2}+4 p=0$
$\therefore \quad y-p x=2 \sqrt{-p}$
$\Rightarrow \quad y=p x+2 \sqrt{-p}$
On differentiating w.r.t. $x$, we get
$$ \begin{array}{rlrl} & & p=p+\frac{d p}{d x} \cdot x+2 \cdot \frac{1}{2}(-p)^{-1 / 2} \cdot(-1) \frac{d p}{d x} \\ \Rightarrow & \frac{d p}{d x}{x-(-p)^{-1 / 2} }=0 \\ \Rightarrow & \frac{d p}{d x} & =0 \quad \text { or } \quad x=(-p)^{-1 / 2} \\ \text { If } & \frac{d p}{d x} & =0 \Rightarrow p=c \end{array} $$
On putting this value in Eq. (i), we get $y=c x+2 \sqrt{-c}$
This curve passes through $(1,1)$.
$$ \begin{aligned} \Rightarrow & & 1 & =c+2 \sqrt{-c} \\ \Rightarrow & & c & =-1 \\ & \therefore & y & =-x+2 \\ \Rightarrow & & x+y & =2 \end{aligned} $$
Again, if $\quad x=(-p)^{-1 / 2}$
$\Rightarrow-p=\frac{1}{x^{2}}$ putting in Eq. (i)
$$ y=\frac{-x}{x^{2}}+2 \cdot \frac{1}{x} \Rightarrow x y=1 $$
Thus, the two curves are $x y=1$ and $x+y=2$.
