Differential Equations 1 Question 18
18. Let
Integer Answer Type Question
Show Answer
Answer:
Correct Answer: 18. (b)
Solution:
- Equation of tangent to the curve
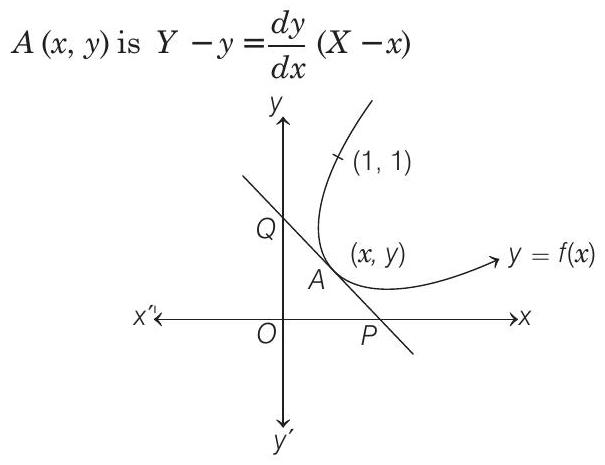
whose,
Given,
On differentiating w.r.t.
On putting this value in Eq. (i), we get
This curve passes through
Again, if
Thus, the two curves are






