Differential Equations 1 Question 11
11. Let $f:[0, \infty) \rightarrow R$ be a continuous function such that $f(x)=1-2 x+\int _0^{x} e^{x-t} f(t) d t$ for all $x \in[0, \infty)$. Then, which of the following statement(s) is (are) TR10018Adv.)
(a) The curve $y=f(x)$ passes through the point $(1,2)$
(b) The curve $y=f(x)$ passes through the point $(2,-1)$
(c) The area of the region ${(x, y) \in[0,1] \times R: f(x) \leq y \leq \sqrt{1-x^{2}} }$ is $\frac{\pi-2}{4}$
(d) The area of the region ${(x, y) \in[0,1] \times R: f(x) \leq y \leq \sqrt{1-x^{2}} }$ is $\frac{\pi-1}{4}$
Show Answer
Answer:
Correct Answer: 11. (b)
Solution:
- We have,
$$ f(x)=1-2 x+\int _0^{x} e^{x-t} f(t) d t $$
On multiplying $e^{-x}$ both sides, we get
$$ e^{-x} f(x)=e^{-x}-2 x e^{-x}+\int _0^{x} e^{-t} f(t) d t $$
On differentiating both side w.r.t. $x$, we get
$$ e^{-x} f^{\prime}(x)-e^{-x} f(x)=-e^{-x}-2 e^{-x}+2 x e^{-x}+e^{-x} f(x) $$
$\Rightarrow \quad f^{\prime}(x)-2 f(x)=2 x-3$
$\begin{array}{rlrl}\text { Let } & & f(x) & =y \ \Rightarrow & f^{\prime}(x) & =\frac{d y}{d x}\end{array}$
[dividing both sides by $e^{-x}$ ]
$\therefore \frac{d y}{d x}-2 y=2 x-3$
which is linear differential equation of the form $\frac{d y}{d x}+P y=Q$. Here, $P=-2$ and $Q=2 x-3$.
Now, $\quad$ IF $=e^{\int P d x}=e^{\int-2 d x}=e^{-2 x}$
$\therefore$ Solution of the given differential equation is
$$ \begin{aligned} & y \cdot e^{-2 x}=\int \begin{array}{c} (2 x-3) e^{-2 x} \\ \text { II } \end{array} d x+C \\ & y \cdot e^{-2 x}=\frac{-(2 x-3) \cdot e^{-2 x}}{2}+2 \int \frac{e^{-2 x}}{2} d x+C \end{aligned} $$
[by using integration by parts]
$\Rightarrow y \cdot e^{-2 x}=\frac{-(2 x-3) e^{-2 x}}{2}-\frac{e^{-2 x}}{2}+C$
$\Rightarrow y=(1-x)+C e^{2 x}$
On putting $x=0$ and $y=1$, we get
$$ 1=1+C \Rightarrow C=0 $$
$\therefore \quad y=1-x$
$y=1-x$ passes through $(2,-1)$
Now, area of region bounded by curve $\quad y=\sqrt{1-x^{2}}$ and $y=1-x$ is shows as
$\therefore$ Area of shaded region
$=$ Area of 1 st quadrant of a circle - Area of $\triangle O A B$
$$ \begin{aligned} & =\frac{\pi}{4}(1)^{2}-\frac{1}{2} \times 1 \times 1 \\ & =\frac{\pi}{4}-\frac{1}{2}=\frac{\pi-2}{4} \end{aligned} $$
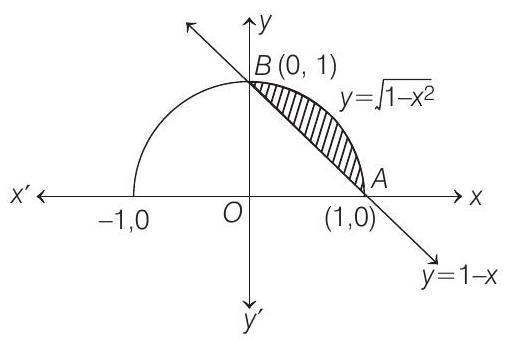
Hence, options $b$ and $c$ are correct.
