Differential Equations 1 Question 11
11. Let
(a) The curve
(b) The curve
(c) The area of the region
(d) The area of the region
Show Answer
Answer:
Correct Answer: 11. (b)
Solution:
- We have,
On multiplying
On differentiating both side w.r.t.
[dividing both sides by
which is linear differential equation of the form
Now,
[by using integration by parts]
On putting
Now, area of region bounded by curve
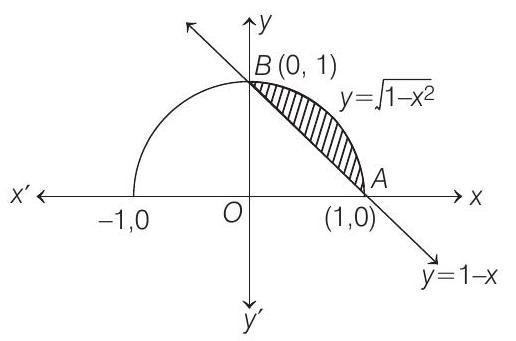
Hence, options






