Complex Numbers 4 Question 6
6.
The complex numbers $z _1, z _2$ and $z _3$ satisfying $\frac{z _1-z _3}{z _2-z _3}=\frac{1-i \sqrt{3}}{2}$ are the vertices of a triangle which is
(a) of area zero
(b) right angled isosceles
(c) equilateral
(d) obtuse angled isosceles
Show Answer
Answer:
Correct Answer: 6. (c)
Solution:
- $\frac{z _1-z _3}{z _2-z _3}=\frac{1-i \sqrt{3}}{2}=\frac{(1-i \sqrt{3})(1+i \sqrt{3})}{2(1+i \sqrt{3})}$
$=\frac{1-i^{2} 3}{2(1+i \sqrt{3})}$
$=\frac{4}{2(1+i \sqrt{3})}$
$=\frac{2}{(1+i \sqrt{3})}$
$\Rightarrow \quad \frac{z _2-z _3}{z _1-z _3}=\frac{1+i \sqrt{3}}{2}=\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}$
$\Rightarrow \quad \frac{z _2-z _3}{z _1-z _3}=1$ and $\arg \frac{z _2-z _3}{z _1-z _3}=\frac{\pi}{3}$
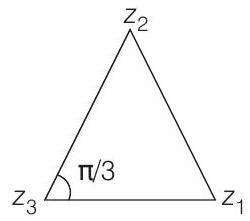
Hence, the triangle is an equilateral.
Alternate Solution
$ \begin{array}{ll} \therefore \frac{z _1-z _3}{z _2-z _3}=\frac{1-i \sqrt{3}}{2} \\ \Rightarrow \quad \frac{z _2-z _3}{z _1-z _3}=\frac{2}{1-i \sqrt{3}}=\frac{1+i \sqrt{3}}{2}=\cos \frac{\pi}{3}+i \sin \frac{\pi}{3} \\ \Rightarrow \quad \arg \frac{z _2-z _3}{z _1-z _3}=\frac{\pi}{3} \text { and also }\left|\frac{z _2-z _3}{z _1-z _3}\right|=1 \end{array} $
Therefore, triangle is equilateral.
