Complex Numbers 4 Question 16
16. Show that the area of the triangle on the argand diagram formed by the complex number
(1986,
Show Answer
Solution:
- We have,
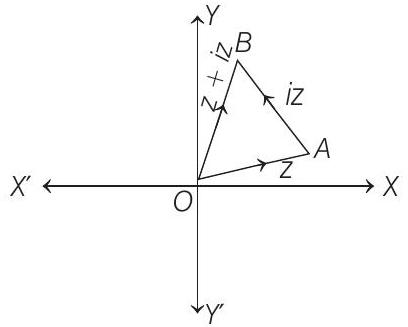
Area of






