Complex Numbers 4 Question 12
12. If one of the vertices of the square circumscribing the circle
(2005, 4M)
Show Answer
Answer:
Correct Answer: 12.
Solution:
- Here, centre of circle is
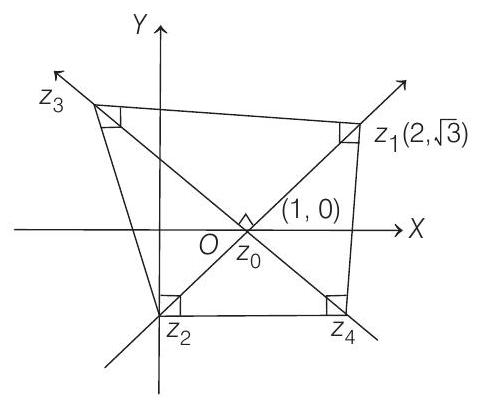
and






