Complex Numbers 4 Question 10
10. $A B C D$ is a rhombus. Its diagonals $A C$ and $B D$ intersect at the point $M$ and satisfy $B D=2 A C$. If the points $D$ and $M$ represent the complex numbers $1+i$ and $2-i$ respectively, then $A$ represents the complex number …or…
(1993, 2M)
Show Answer
Answer:
Correct Answer: 10. $3-\frac{i}{2}$ or $1-\frac{3 i}{2}$
Solution:
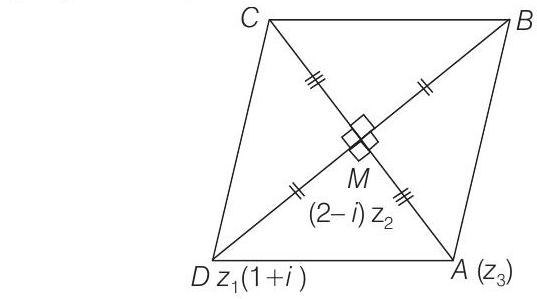
- Given, $D=(1+i), M=(2-i)$
and diagonals of a rhombus bisect each other.
Let $B \equiv(a+i b)$, therefore
$$ \begin{array}{rlrl} & & \frac{a+1}{2}=2, \frac{b+1}{2} & =-1 \\ \Rightarrow & & a+1=4, b+1 & =-2 \Rightarrow a=3, b=-3 \\ \Rightarrow & B & \equiv(3-3 i) \end{array} $$
Again, $\quad D M=\sqrt{(2-1)^{2}+(-1-1)^{2}}=\sqrt{1+4}=\sqrt{5}$
But $B D=2 D M \quad \Rightarrow \quad B D=2 \sqrt{5}$
and $\quad 2 A C=B D \quad \Rightarrow \quad 2 A C=2 \sqrt{5}$
$\Rightarrow \quad A C=\sqrt{5}$ and $\quad A C=2 A M$
$\Rightarrow \quad \sqrt{5}=2 A M \quad \Rightarrow \quad A M=\frac{\sqrt{5}}{2}$
Now, let coordinate of $A$ be $(x+i y)$.
But in a rhombus $A D=A B$, therefore we have
$A D^{2}=A B^{2}$
$\Rightarrow \quad(x-1)^{2}+(y-1)^{2}=(x-3)^{2}+(y+3)^{2}$
$\Rightarrow \quad x^{2}+1-2 x+y^{2}+1-2 y=x^{2}+9-6 x+y^{2}+9+6 y$
$\Rightarrow \quad 4 x-8 y=16$
$\Rightarrow \quad x-2 y=4$
$\Rightarrow \quad x=2 y+4$
Again, $\quad A M=\frac{\sqrt{5}}{2} \Rightarrow A M^{2}=\frac{5}{4}$
$\Rightarrow \quad(x-2)^{2}+(y+1)^{2}=\frac{5}{4}$
$\Rightarrow \quad(2 y+2)^{2}+(y+1)^{2}=\frac{5}{4} \quad$ [from Eq. (i)]
$\Rightarrow \quad 5 y^{2}+10 y+5=\frac{5}{4}$
$\Rightarrow \quad 20 y^{2}+40 y+15=0$
$\Rightarrow \quad 4 y^{2}+8 y+3=0$
$\Rightarrow \quad(2 y+1)(2 y+3)=0$
$\Rightarrow \quad 2 y+1=0,2 y+3=0$
$\Rightarrow \quad y=-\frac{1}{2}, y=-\frac{3}{2}$
On putting these values in Eq. (i), we get
$$ \begin{aligned} & & x=2-\frac{1}{2}+4, x=2 \quad-\frac{3}{2}+4 \\ \Rightarrow & & x=3, x=1 \end{aligned} $$
Therefore, $A$ is either $3-\frac{i}{2}$ or $1-\frac{3 i}{2}$.
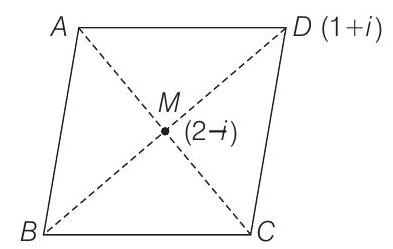
Alternate Solution
Since, $M$ is the centre of rhombus.
$\therefore$ By rotating $D$ about $M$ through an angle of $\pm \pi / 2$, we get possible position of $A$.
$\Rightarrow \frac{z _3-(2-i)}{-1+2 i}=\frac{1}{2}( \pm i) \quad \Rightarrow \quad \frac{z _3-(2-i)}{-1+2 i}=\frac{1}{2}( \pm i)$
$$ \begin{aligned} \Rightarrow z _3 & =(2-i) \pm \frac{1}{2} i(2 i-1)=(2-i) \pm \frac{1}{2}(-2-i) \\ & =\frac{(4-2 i-2-i)}{2}, \frac{4-2 i+2+i}{2}=1-\frac{3}{2} i, 3-\frac{i}{2} \end{aligned} $$
$\therefore A$ is either $1-\frac{3}{2} i$ or $3-\frac{i}{2}$.
