Circle 5 Question 4
4. The locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line
(2012)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 4. (a)
Solution:
- PLAN If
Description of Situation As equation of chord of contact is
Here, equation of chord of contact w.r.t.
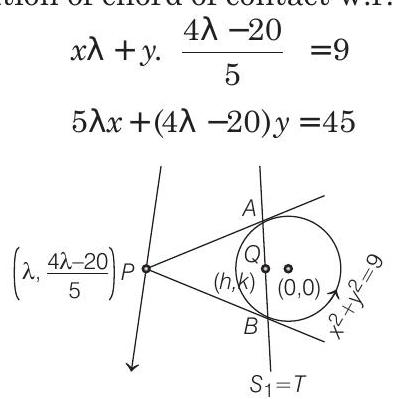
and equation of chord bisected at the point
From Eqs. (i) and (ii), we get






