Circle 5 Question 4
4. The locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line $4 x-5 y=20$ to the circle $x^{2}+y^{2}=9$ is
(2012)
(a) $20\left(x^{2}+y^{2}\right)-36 x+45 y=0$
(b) $20\left(x^{2}+y^{2}\right)+36 x-45 y=0$
(c) $36\left(x^{2}+y^{2}\right)-20 y+45 y=0$
(d) $36\left(x^{2}+y^{2}\right)+20 x-45 y=0$
Show Answer
Answer:
Correct Answer: 4. (a)
Solution:
- PLAN If $S: a x^{2}+2 h x y+b y^{2}+2 g x+2 f y+C$ then equation of chord bisected at $P\left(x _1, y _1\right)$ is $T=S _1$ or a $x x _1+h\left(x y _1+y x _1\right)+b y y _1+g\left(x+x _1\right)+f\left(y+y _1\right)+C$ $=a x _1^{2}+2 h x _1 y _1+b y _1^{2}+2 g x _1+2 f y _1+C$
Description of Situation As equation of chord of contact is $T=0$
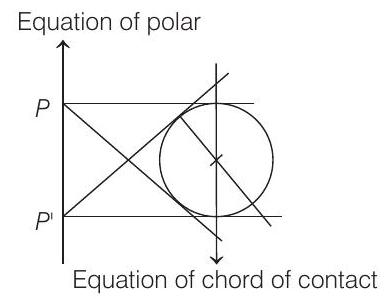
Here, equation of chord of contact w.r.t. $P$ is
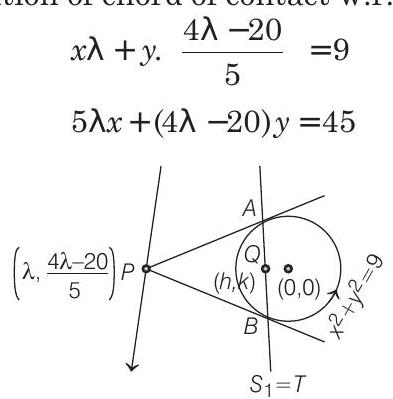
and equation of chord bisected at the point $Q(h, k)$ is
$$ \begin{aligned} & & x h+y k-9 & =h^{2}+k^{2}-9 \\ \Rightarrow & & x h+k y & =h^{2}+k^{2} \end{aligned} $$
From Eqs. (i) and (ii), we get
$$ \begin{aligned} & & \frac{5 \lambda}{h} & =\frac{4 \lambda-20}{k}=\frac{45}{h^{2}+k^{2}} \\ & \therefore & \lambda & =\frac{20 h}{4 h-5 k} \text { and } \lambda=\frac{9 h}{h^{2}+k^{2}} \\ & \Rightarrow & \frac{20 h}{4 h-5 k} & =\frac{9 h}{h^{2}+k^{2}} \\ & \text { or } & 20\left(h^{2}+k^{2}\right) & =9(4 h-5 k) \\ & \text { or } & 20\left(x^{2}+y^{2}\right) & =36 x-45 y \end{aligned} $$
