Circle 5 Question 18
18. $C _1$ and $C _2$ are two concentric circles, the radius of $C _2$ being twice that of $C _1$. From a point $P$ on $C _2$, tangents $P A$ and $P B$ are drawn to $C _1$. Prove that the centroid of the $\triangle P A B$ lies on $C _1$.
$(1998,8$ M)
Show Answer
Solution:
- Let the coordinate of point $P$ be $(2 r \cos \theta, 2 r \sin \theta)$
We have, $O A=r, O P=2 r$
Since, $\triangle O A P$ is a right angled triangle.
Circle 415
$\cos \varphi=1 / 2 \Rightarrow \varphi=\pi / 3$
$\therefore$ Coordinates of $A$ are ${r \cos (\theta-\pi / 3), r \sin (\theta-\pi / 3)}$
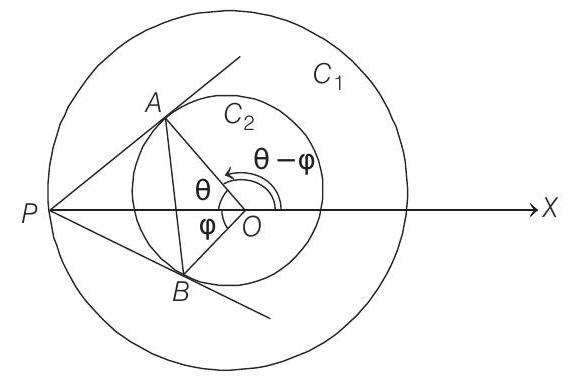
and that of $B$ are $[r \cos (\theta+\pi / 3), r \sin (\theta+\pi / 3)]$
If $p, q$ is the centroid of $\triangle P A B$, then $p=\frac{1}{3}[r \cos (\theta-\pi / 3)+r \cos (\theta+\pi / 3)+2 r \cos \theta]$
$=\frac{1}{3}[r{\cos (\theta-\pi / 3)+\cos (\theta+\pi / 3)}+2 r \cos \theta]$
$=\frac{1}{3} r 2 \cos \frac{\theta-\frac{\pi}{3}+\theta+\frac{\pi}{3}}{2} \cdot \cos \frac{\theta-\frac{\pi}{3}-\theta-\frac{\pi}{3}}{2}+2 r \cos \theta$
$=\frac{1}{3}[r{2 \cos \theta \cos \pi / 3}+2 r \cos \theta]$
$=\frac{1}{3}[r \cdot \cos \theta+2 r \cos \theta]=r \cos \theta$
and $q=\frac{1}{3}\left[r \sin \theta-\frac{\pi}{3}+r \sin \theta+\frac{\pi}{3}+2 r \sin \theta\right]$
$=\frac{1}{3}\left[r{\sin \theta-\frac{\pi}{3}+\sin \theta+\frac{\pi}{3} }+2 r \sin \theta\right]$
$=\frac{1}{3} r 2 \sin \frac{\theta-\frac{\pi}{3}+\theta+\frac{\pi}{3}}{2} \cdot \cos \frac{\theta-\frac{\pi}{3}-\theta-\frac{\pi}{3}}{2}+2 r \sin \theta$
$=\frac{1}{3}[r(2 \sin \theta \cos \pi / 3)+2 r \sin \theta]$
$=\frac{1}{3}[r(\sin \theta)+2 r \sin \theta]=r \sin \theta$
Now, $(p, q)=(r \cos \theta, r \sin \theta)$ lies on $x^{2}+y^{2}=r^{2}$ which is called $C _1$.
