Circle 2 Question 22
23. Three circles touch one another externally. The tangents at their points of contact meet at a point whose distance from a point of contact is 4 . Find the ratio of the product of the radii to the sum of the radii of the circles.
$(1992,5$ M)
Show Answer
Solution:
- Suppose the circles have centres at $C _1, C _2$ and $C _3$ with radius $R _1, R _2$ and $R _3$, respectively. Let the circles touch at $A, B$ and $C$. Let the common tangents at $A, B$ and $C$ meet at $O$. We have, $O A=O B=O C=4$ [given]. Now, the circle with centre at $O$ and passing through $A, B$ and $C$ is the incircle of the triangle $C _1 C _2 C _3$ (because $O A \perp C _1 C _2$ ).
Therefore, the inradius of $\Delta C _1 C _2 C _3$ is 4 .
and
$$ r=\frac{\Delta}{s} $$
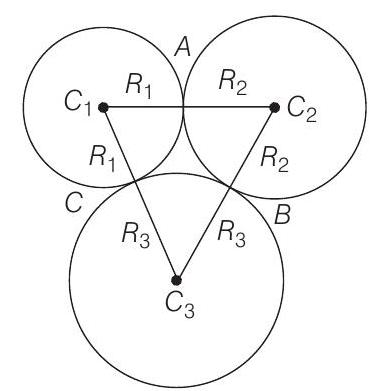
Now, perimeter of a triangle
$$ \begin{aligned} & 2 s=R _1+R _2+R _2+R _3+R _3+R _1 \\ & \Rightarrow \quad 2 s=2\left(R _1+R _2+R _3\right) \\ & \Rightarrow \quad s=R _1+R _2+R _3 \\ & \text { and } \quad \Delta=\sqrt{s(s-a)(s-b)(s-c)} \\ & =\sqrt{\left(R _1+R _2+R _3\right)\left(R _3\right)\left(R _2\right)\left(R _1\right)} \\ & \text { From Eq. (i), } \quad 4=\frac{\sqrt{R _1 R _2 R _3\left(R _1+R _2+R _3\right)}}{R _1+R _2+R _3} \\ & \begin{array}{rlrl} & \Rightarrow & 16 & =\frac{R _1 R _2 R _3\left(R _1+R _2+R _3\right)}{\left(R _1+R _2+R _3\right)^{2}} \\ \Rightarrow & 16 & =\frac{R _1 R _2 R _3}{R _1+R _2+R _3} \end{array} \end{aligned} $$
