Circle 2 Question 22
23. Three circles touch one another externally. The tangents at their points of contact meet at a point whose distance from a point of contact is 4 . Find the ratio of the product of the radii to the sum of the radii of the circles.
Show Answer
Solution:
- Suppose the circles have centres at
Therefore, the inradius of
and
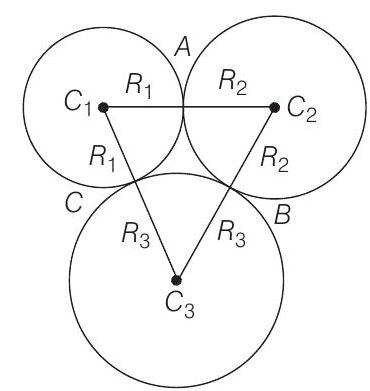
Now, perimeter of a triangle






