Circle 2 Question 12
13. The angle between a pair of tangents drawn from a point
is
(1996, 1M)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 13. (d)
Solution:
- Centre of the circle
is
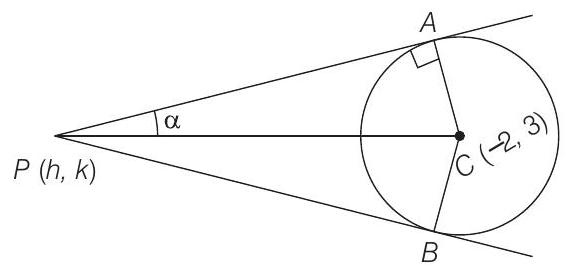
Let
That is, triangle
Thus, required equation of the locus is






