####59. A swimmer is in the sea at a distance from the closest point on a straight shore. The house of the swimmer is on the shore at a distance from . He can swim at a speed of and walk at a speed of . At what point on the shore should be land so that he reaches his house in the shortest possible time?
(1983, 2M)
Show Answer
Answer:
Correct Answer: 59. (1)
Solution:
- Let the house of the swimmer be at .
Let the swimmer land at on the shore and let
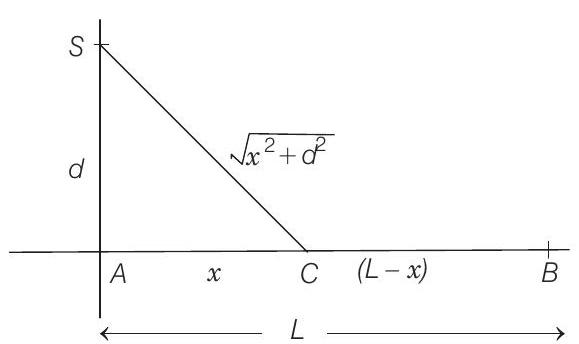
Time from to Time from to Time from to
Let
For maximum or minimum, put
at
But
We consider,
Now,
Hence, has minimum at .







