Application of Derivatives 4 Question 56
59. A swimmer
(1983, 2M)
Show Answer
Answer:
Correct Answer: 59. (1)
Solution:
- Let the house of the swimmer be at
Let the swimmer land at
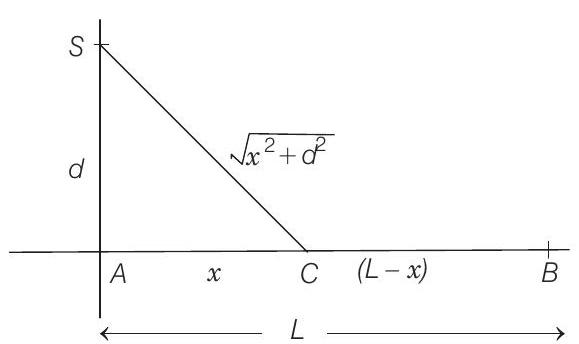
Time from
Let
For maximum or minimum, put
But
Now,
Hence,






