SATHEE: Application of Derivatives 4 Question 51

Application of Derivatives 4 Question 51

####54. A point $P$ is given on the circumference of a circle of radius $r$ . Chord $Q R$ is parallel to the tangent at $P$ . Determine the maximum possible area of the $△ P Q R$ .

$(1990, 4 M)$

Show Answer

Answer:

Correct Answer: 54. (4)

Solution:

Since, the chord $Q R$ is parallel to the tangent at $P$ .

$∴ O N ⊥ Q R$

Consequently, $N$ is the mid-point of chord $Q R$ .

$\begin{aligned} ∴ Q R = 2 Q N = 2 r \sin θ \\ Also, O N = r \cos θ \\ ∴ P N = r + r \cos θ \end{aligned}$

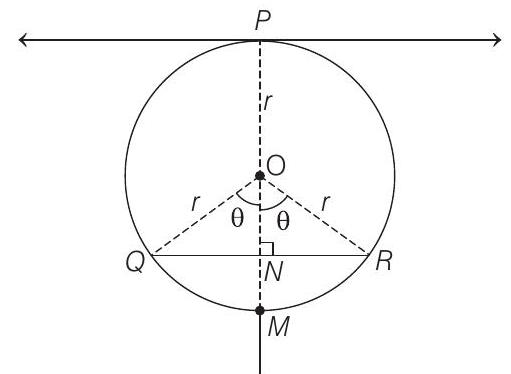
Let $A$ denotes the area of $△ P Q R$ .

Then, $A = \frac{1}{2} \cdot 2 r \sin θ (r + r \cos θ)$

$\Rightarrow A = r^{2} (\sin θ + \sin θ \cos θ)$

$\Rightarrow A = r^{2} (\sin θ + \frac{1}{2} \sin 2 θ)$

$\Rightarrow \frac{d A}{d θ} = r^{2} (\cos θ + \cos 2 θ)$

and $\frac{d^{2} A}{d θ^{2}} = r^{2} (- \sin θ - 2 \sin 2 θ)$

For maximum and minimum values of $θ$ , we put $\frac{d A}{d θ} = 0$

$\Rightarrow \cos θ + \cos 2 θ = 0 \Rightarrow \cos 2 θ = - \cos θ$

$\Rightarrow \cos θ = \cos (π - 2 θ) \Rightarrow θ = \frac{π}{3}$

Clearly, $\frac{d^{2} A}{d θ^{2}} < 0$ for $θ = \frac{π}{3}$

Hence, the area of $△ P Q R$ is maximum when $θ = \frac{π}{3}$ .

The maximum area of $△ P Q R$ is given by

$\begin{aligned} A = r^{2} & \sin \frac{π}{3} + \frac{1}{2} \sin \frac{2 π}{3} = r^{2} \frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{4} \\ = \frac{3 \sqrt{3}}{4} r^{2} sq units \end{aligned}$

Application of Derivatives 4 Question 51

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Application of Derivatives 4 Question 51

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu