Application of Derivatives 4 Question 51
54. A point
Show Answer
Answer:
Correct Answer: 54. (4)
Solution:
- Since, the chord
Consequently,
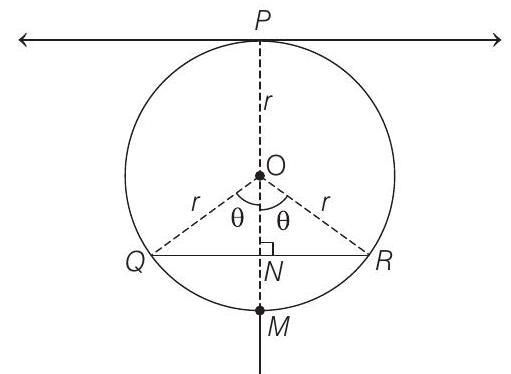
Let
Then,
and
For maximum and minimum values of
Clearly,
Hence, the area of
The maximum area of






