Application of Derivatives 4 Question 44
####46. Let $C_{1}$ and $C_{2}$ be respectively, the parabolas $x^{2}=y-1$ and $y^{2}=x-1$. Let $P$ be any point on $C_{1}$ and $Q$ be any point on $C_{2}$. If $P_{1}$ and $Q_{1}$ is the reflections of $P$ and $Q$, respectively, with respect to the line $y=x$. Prove that $P_{1}$ lies on $C_{2} Q_{1}$ lies on $C_{1}$ and $P Q \geq \min \left(P P_{1}, Q Q_{1}\right)$. Hence, determine points $P_{0}$ and $Q_{0}$ on the parabolas $C_{1}$ and $C_{2}$ respectively such that $P_{0} Q_{0} \leq P Q$ for all pairs of points $(P, Q)$ with $P$ on $C_{1}$ and $Q$ on $C_{2}$.
Show Answer
Answer:
Correct Answer: 46. $b \in(-2,-1) \cup[1, \infty]$
Solution:
- Let coordinates of $P$ be $\left(t, t^{2}+1\right)$
Reflection of $P$ in $y=x$ is $P_{1}\left(t^{2}+1, t\right)$
which clearly lies on $y^{2}=x-1$
Similarly, let coordinates of $Q$ be $\left(s^{2}+1, s\right)$
Its reflection in $y=x$ is
$Q_{1}\left(s, s^{2}+1\right)$, which lies on $x^{2}=y-1$.
We have, $\quad P Q_{1}^{2}=(t-s)^{2}+\left(t^{2}-s^{2}\right)^{2}=P_{1} Q^{2}$
$\Rightarrow \quad P Q_{1}=P_{1} Q$
Also $P P_{1} | Q Q_{1} \quad[\because$ both perpendicular to $y=x]$
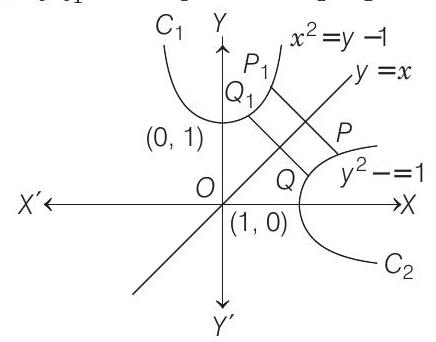
Thus, $P P_{1} Q Q_{1}$ is an isosceles trapezium.
Also, $P$ lies on $P Q_{1}$ and $Q$ lies on $P_{1} Q$, then
$P Q \geq \min \left{P P_{1} Q Q_{1}\right}$
Let us take $\min \left{P P_{1} Q Q_{1}\right}=P P_{1}$
$\therefore \quad P Q^{2} \geq P P_{1}^{2}=\left(t^{2}+1-t\right)^{2}+\left(t^{2}+1-t^{2}\right)$
$ =2\left(t^{2}+1-t^{2}\right)=f(t) $
[say] we have, $f^{\prime}(t)=4\left(t^{2}+1-t\right)(2 t-1)$
$ =4\left[(t-1 / 2)^{2}+3 / 4\right][2 t-1] $
Now, $\quad f^{\prime}(t)=0$
$\Rightarrow \quad t=1 / 2$
Also, $f^{\prime}(t)<0$ for $t<1 / 2$
and $f^{\prime}(t)>0$ for $t>1 / 2$
Thus, $f(t)$ is least when $t=1 / 2$.
Corresponding to $t=1 / 2$, point $P_{0}$ on $C_{1}$ is $(1 / 2,5 / 4)$ and $P_{1}$ (which we take as $Q_{0}$ ) on $C_{2}$ are $(5 / 4,1 / 2)$. Note that $P_{0} Q_{0} \leq P Q$ for all pairs of $(P, Q)$ with $P$ on $C_{2}$.
