Application of Derivatives 4 Question 44
46. Let
Show Answer
Answer:
Correct Answer: 46.
Solution:
- Let coordinates of
Reflection of
which clearly lies on
Similarly, let coordinates of
Its reflection in
We have,
Also
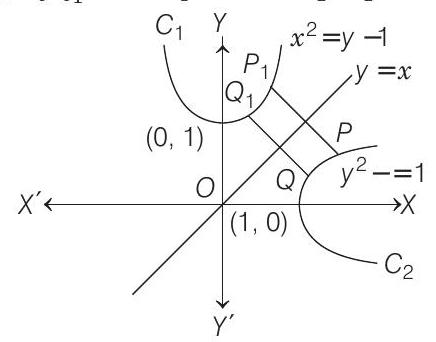
Thus,
Also,
Let us take
[say] we have,
Now,
Also,
and
Thus,
Corresponding to






