Application of Derivatives 4 Question 36
####38. A line $L: y=m x+3$ meets $Y$-axis at $E(0,3)$ and the arc of the parabola $y^{2}=16 x, 0 \leq y \leq 6$ at the point $F\left(x_{0}, y_{0}\right)$. The tangent to the parabola at $F\left(x_{0}, y_{0}\right)$ intersects the $Y$-axis at $G\left(0, y_{1}\right)$. The slope $m$ of the line $L$ is chosen such that the area of the $\triangle E F G$ has a local maximum
Match List I with List II and select the correct answer using the codes given below the list.
| Column I | Column II | ||
|---|---|---|---|
| P. | $m=$ | 1. | $1 / 2$ |
| Q. | Maximum area | 2. | 4 |
| of $\triangle F F G$ is |
Codes
| $\mathrm{P}$ | $\mathrm{Q}$ | $\mathrm{R}$ | $\mathrm{S}$ | |
|---|---|---|---|---|
| (a) | 4 | 1 | 2 | 3 |
| (b) | 3 | 4 | 1 | 2 |
| (c) | 1 | 3 | 2 | 4 |
| (d) | 1 | 3 | 4 | 2 |
Passage Based Problems
Consider the function $f:(-\infty, \infty) \rightarrow(-\infty, \infty)$ defined by $f(x)=\frac{x^{2}-a x+1}{x^{2}+a x+1} ; 0<a<2$.
$(2008,12 \mathrm{M})$
Show Answer
Answer:
Correct Answer: 38. (a)
Solution:
- Here, $y^{2}=16 x, 0 \leq y \leq 6$
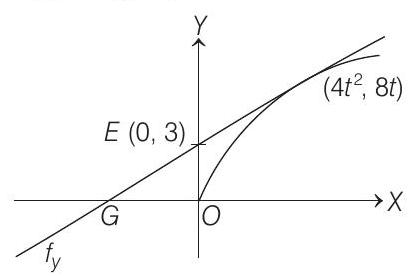
Tangent at $F, \quad y t=x+a t^{2}$
At $\quad x=0, y=a t=4 t$
Also, $\left(4 t^{2}, 8 t\right)$ satisfy $y=m x+c$.
$ \begin{array}{rlrl} & \Rightarrow & 8 t & =4 m t^{2}+3 \\ & \Rightarrow & 4 m t^{2}-8 t+3 & =0 \\ & \therefore & \text { Area of } \Delta & =\frac{1}{2}\left|\begin{array}{ccc} 0 & 3 & 1 \\ 0 & 4 t & 1 \\ 4 t^{2} & 8 t & 1 \end{array}\right|=\frac{1}{2} \cdot 4 t^{2}(3-4 t) \\ & \therefore & & =2\left[3 t^{2}-4 t^{3}\right] \\ & & \frac{d A}{d t} & =2\left[6 t-12 t^{2}\right]=-12 t(12 t-1) \\ & & \frac{1}{2}+\frac{1}{2} \end{array} $
$\therefore$ Maximum at $t=\frac{1}{2}$ and $4 m t^{2}-8 t+3=0$
$ \begin{array}{rlrl} & \Rightarrow & m-4+3 & =0 \\ & \Rightarrow & m & =1 \\ \Rightarrow \quad G(0,4 t) & \Rightarrow G(0,2) \\ & & y_{1} & =2 \\ & & \left.x_{0}, y_{0}\right)=\left(4 t^{2}, 8 t\right) & =(1,4) \\ y_{0} & =4 \\ & & \text { Area } & =2 \frac{3}{4}-\frac{1}{2}=\frac{1}{2} \end{array} $
