SATHEE: Application of Derivatives 4 Question 25

Application of Derivatives 4 Question 25

####26. Find the coordinates of all the points $P$ on the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ , for which the area of the $△ P O N$ is maximum, where $O$ denotes the origin and $N$ is the foot of the perpendicular from $O$ to the tangent at $P$ .

(a) $\frac{\pm a^{2}}{\sqrt{a^{2} + b^{2}}}, \frac{\pm b^{2}}{\sqrt{a^{2} + b^{2}}}$

(b) $\frac{\pm a^{2}}{\sqrt{a^{2} - b^{2}}}, \frac{\pm b^{2}}{\sqrt{a^{2} - b^{2}}}$

(d) $\frac{\pm a^{2}}{\sqrt{a^{2} - b^{2}}}, \frac{\pm b^{2}}{\sqrt{a^{2} + b^{2}}}$

$(1990, 10 M)$

Show Answer

Answer:

Correct Answer: 26. (b, c)

Solution:

Let the coordinates of $P$ be $(a \cos θ, b \sin θ)$

Equations of tangents at $P$ is

$\frac{x}{a} \cos θ + \frac{y}{b} \sin θ = 1$

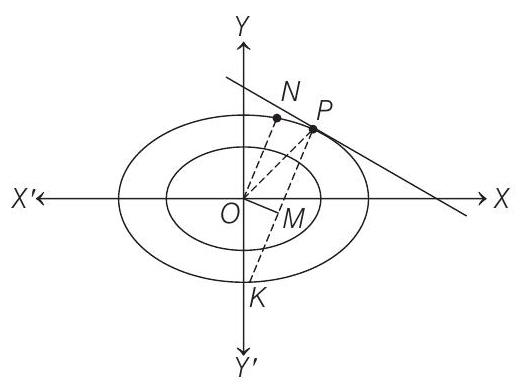
Again, equation of normal at point $P$ is

$a x \sec θ - b y cosec θ = a^{2} - b^{2}$

Let $M$ be foot of perpendicular from $O$ to $P K$ , the normal at $P$ .

Area of $△ O P N = \frac{1}{2}$ (Area of rectangle $O M P N$ )

$= \frac{1}{2} O N \cdot O M$

Now, $O N = \frac{1}{\sqrt{\frac{\cos^{2} θ}{a^{2}} + \frac{\sin^{2} θ}{b^{2}}}} = \frac{a b}{\sqrt{b^{2} \cos^{2} θ + a^{2} \sin^{2} θ}}$

[perpendicular from $O$ , to line $N P$ ]

and $O M = \frac{a^{2} - b^{2}}{\sqrt{a^{2} \sec^{2} θ + b^{2} {cosec}^{2} θ}} = \frac{(a^{2} - b^{2}) \cdot \cos θ \cdot \sin θ}{\sqrt{a^{2} \sin^{2} θ + b^{2} \cos^{2} θ}}$

Thus, area of $△ O P N = \frac{a b (a^{2} - b^{2}) \cos θ \cdot \sin θ}{2 (a^{2} \sin^{2} θ + b^{2} \cos^{2} θ)}$

$= \frac{a b (a^{2} - b^{2}) \tan θ}{2 (a^{2} \tan^{2} θ + b^{2})}$

$\begin{aligned} Let f (θ) & = \frac{\tan θ}{α^{2} \tan^{2} θ + b^{2}} [0 < θ < π / 2] \\ f^{'} (θ) & = \frac{\sec^{2} θ (a^{2} \tan^{2} θ + b^{2}) - \tan θ (2 a^{2} \tan θ \sec^{2} θ)}{{(a^{2} \tan^{2} θ + b^{2})}^{2}} \\ = \frac{\sec^{2} θ (a^{2} \tan^{2} θ + b^{2} - 2 a^{2} \tan^{2} θ)}{{(a^{2} \tan^{2} θ + b^{2})}^{2}} \\ = \frac{\sec^{2} θ (a \tan θ + b) (b - a \tan θ)}{{(a^{2} \tan^{2} θ + b^{2})}^{2}} \end{aligned}$

For maximum or minimum, we put

$\begin{array}{cc} f^{'} (θ) = 0 \Rightarrow b - a \tan θ = 0 \\ [\sec^{2} θ \neq 0, a \tan θ + b \neq 0, 0 < θ < π / 2] \\ \Rightarrow & \tan θ = b / a \end{array}$

Also, $f^{'} (θ)$

0 \text {, if } 0<\theta<\tan ^{-1}(b / a) $

$< 0, if \tan^{- 1} (b / a) < θ < π / 2$

Therefore, $f (θ)$ has maximum, when

$θ = \tan^{- 1} \frac{b}{a} \Rightarrow \tan θ = \frac{b}{a}$

Again, $\sin θ = \frac{b}{\sqrt{a^{2} + b^{2}}}, \cos θ = \frac{a}{\sqrt{a^{2} + b^{2}}}$

By using symmetry, we get the required points

$\frac{\pm a^{2}}{\sqrt{a^{2} + b^{2}}}, \frac{\pm b^{2}}{\sqrt{a^{2} + b^{2}}}$

Application of Derivatives 4 Question 25

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Application of Derivatives 4 Question 25

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu