Application of Derivatives 4 Question 25
26. Find the coordinates of all the points $P$ on the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$, for which the area of the $\triangle P O N$ is maximum, where $O$ denotes the origin and $N$ is the foot of the perpendicular from $O$ to the tangent at $P$.
(a) $\frac{ \pm a^{2}}{\sqrt{a^{2}+b^{2}}}, \frac{ \pm b^{2}}{\sqrt{a^{2}+b^{2}}}$
(b) $\frac{ \pm a^{2}}{\sqrt{a^{2}-b^{2}}}, \frac{ \pm b^{2}}{\sqrt{a^{2}-b^{2}}}$
(c) $\frac{ \pm a^{2}}{\sqrt{a^{2}+b^{2}}}, \frac{ \pm b^{2}}{\sqrt{a^{2}-b^{2}}}$
(d) $\frac{ \pm a^{2}}{\sqrt{a^{2}-b^{2}}}, \frac{ \pm b^{2}}{\sqrt{a^{2}+b^{2}}}$
$(1990,10 M)$
Show Answer
Answer:
Correct Answer: 26. (b, c)
Solution:
- Let the coordinates of $P$ be $(a \cos \theta, b \sin \theta)$
Equations of tangents at $P$ is
$$ \frac{x}{a} \cos \theta+\frac{y}{b} \sin \theta=1 $$
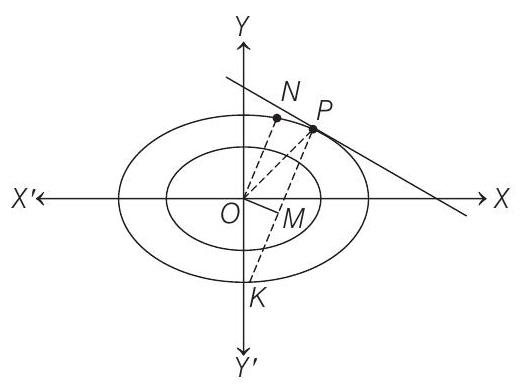
Again, equation of normal at point $P$ is
$$ a x \sec \theta-b y \operatorname{cosec} \theta=a^{2}-b^{2} $$
Let $M$ be foot of perpendicular from $O$ to $P K$, the normal at $P$.
Area of $\triangle O P N=\frac{1}{2}$ (Area of rectangle $O M P N$ )
$$ =\frac{1}{2} O N \cdot O M $$
Now, $\quad O N=\frac{1}{\sqrt{\frac{\cos ^{2} \theta}{a^{2}}+\frac{\sin ^{2} \theta}{b^{2}}}}=\frac{a b}{\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}}$
[perpendicular from $O$, to line $N P$ ]
and $O M=\frac{a^{2}-b^{2}}{\sqrt{a^{2} \sec ^{2} \theta+b^{2} \operatorname{cosec}^{2} \theta}}=\frac{\left(a^{2}-b^{2}\right) \cdot \cos \theta \cdot \sin \theta}{\sqrt{a^{2} \sin ^{2} \theta+b^{2} \cos ^{2} \theta}}$
Thus, area of $\triangle O P N=\frac{a b\left(a^{2}-b^{2}\right) \cos \theta \cdot \sin \theta}{2\left(a^{2} \sin ^{2} \theta+b^{2} \cos ^{2} \theta\right)}$
$$ =\frac{a b\left(a^{2}-b^{2}\right) \tan \theta}{2\left(a^{2} \tan ^{2} \theta+b^{2}\right)} $$
$$ \begin{aligned} \text { Let } f(\theta) & =\frac{\tan \theta}{\alpha^{2} \tan ^{2} \theta+b^{2}} \quad[0<\theta<\pi / 2] \\ f^{\prime}(\theta) & =\frac{\sec ^{2} \theta\left(a^{2} \tan ^{2} \theta+b^{2}\right)-\tan \theta\left(2 a^{2} \tan \theta \sec ^{2} \theta\right)}{\left(a^{2} \tan ^{2} \theta+b^{2}\right)^{2}} \\ & =\frac{\sec ^{2} \theta\left(a^{2} \tan ^{2} \theta+b^{2}-2 a^{2} \tan ^{2} \theta\right)}{\left(a^{2} \tan ^{2} \theta+b^{2}\right)^{2}} \\ & =\frac{\sec ^{2} \theta(a \tan \theta+b)(b-a \tan \theta)}{\left(a^{2} \tan ^{2} \theta+b^{2}\right)^{2}} \end{aligned} $$
For maximum or minimum, we put
$$ \begin{array}{cc} & f^{\prime}(\theta)=0 \Rightarrow \quad b-a \tan \theta=0 \\ & {\left[\sec ^{2} \theta \neq 0, a \tan \theta+b \neq 0,0<\theta<\pi / 2\right]} \\ \Rightarrow \quad & \tan \theta=b / a \end{array} $$
Also, $f^{\prime}(\theta)$
$$
0 \text {, if } 0<\theta<\tan ^{-1}(b / a) $$
$$ <0 \text {, if } \tan ^{-1}(b / a)<\theta<\pi / 2 $$
Therefore, $f(\theta)$ has maximum, when
$$ \theta=\tan ^{-1} \frac{b}{a} \Rightarrow \tan \theta=\frac{b}{a} $$
Again, $\quad \sin \theta=\frac{b}{\sqrt{a^{2}+b^{2}}}, \cos \theta=\frac{a}{\sqrt{a^{2}+b^{2}}}$
By using symmetry, we get the required points
$$ \frac{ \pm a^{2}}{\sqrt{a^{2}+b^{2}}}, \frac{ \pm b^{2}}{\sqrt{a^{2}+b^{2}}} $$
