Application of Derivatives 2 Question 3
####3. A water tank has the shape of an inverted right circular cone, whose semi-vertical angle is $\tan ^{-1} \frac{1}{2}$. Water is poured into it at a constant rate of $5 \mathrm{cu} \mathrm{m} / \mathrm{min}$. Then, the rate (in $\mathrm{m} / \mathrm{min}$ ) at which the level of water is rising at the instant when the depth of water in the tank is $10 \mathrm{~m}$ is
(2019 Main, 9 April II)
(a) $\frac{2}{\pi}$
(b) $\frac{1}{5 \pi}$
(c) $\frac{1}{15 \pi}$
(d) $\frac{1}{10 \pi}$
Show Answer
Answer:
(b)
Solution:
Key Idea Use formula: Volume of cone $=\frac{1}{3} \pi r^{2} h$, where $r=$ radius and $h=$ height of the cone.
Given, semi-vertical angle of right circular cone
$ =\tan ^{-1} \frac{1}{2} $
Let $\quad \alpha=\tan ^{-1} \frac{1}{2}$
$\Rightarrow \quad \tan \alpha=\frac{1}{2}$
$\Rightarrow \quad \frac{r}{h}=\frac{1}{2} \quad$ [from fig. $\tan \alpha=\frac{r}{h}$ ]
$ \Rightarrow \quad r=\frac{1}{2} h $
$\because$ Volume of cone is $(V)=\frac{1}{3} \pi r^{2} h$
$\therefore \quad V=\frac{1}{3} \pi \frac{1}{2} h \quad(h)=\frac{1}{12} \pi h^{3} \quad$ [from Eq. (i)]
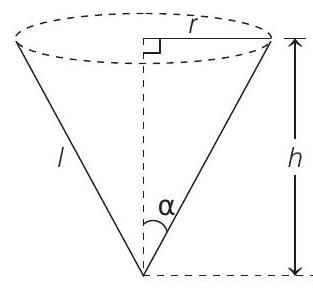
On differentiating both sides w.r.t. ’ $t$ ‘, we get
$ \begin{array}{rlrl} & \frac{d V}{d t} & =\frac{1}{12} \pi\left(3 h^{2}\right) \frac{d h}{d t} \\ \Rightarrow & \frac{d h}{d t} & =\frac{4}{\pi h^{2}} \frac{d V}{d t} \\ \Rightarrow & \frac{d h}{d t} & =\frac{4}{\pi h^{2}} \times 5 & {\left[\because \text { given } \frac{d V}{d t}=5 \mathrm{~m}^{3} / \mathrm{min}\right]} \end{array} $
Now, at $h=10 \mathrm{~m}$, the rate at which height of water level is rising $=\left.\frac{d h}{d t}\right|_{h=10}$
$ =\frac{4}{\pi(10)^{2}} \times 5=\frac{1}{5 \pi} \mathrm{m} / \mathrm{min} $
