Application of Derivatives 2 Question 3
3. A water tank has the shape of an inverted right circular cone, whose semi-vertical angle is
(2019 Main, 9 April II)
(a)
(b)
(c)
(d)
Show Answer
Solution:
Key Idea Use formula:
Volume of cone
Given, semi-vertical angle of right circular cone
Let
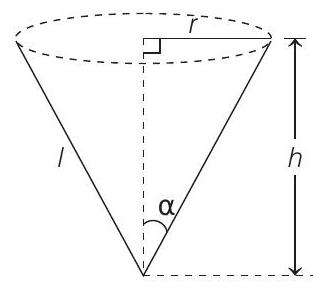
On differentiating both sides w.r.t. ’
Now, at






