Solid State - Result Question 2
####2. An element has a face-centred cubic (fcc) structure with a cell edge of $a$. The distance between the centres of two nearest tetrahedral voids in the lattice is
(2019 Main, 12 April I)
(a) $\sqrt{2} a$
(b) $a$
(c) $\frac{a}{2}$
(d) $\frac{3}{2} a$
Show Answer
Answer:
Correct Answer: 2. (c)
Solution:
- In fcc unit cell, two tetrahedral voids are formed on each of the four non-parallel body diagonals of the cube at a distance of $\sqrt{3} a / 4$ from every corner along the body diagonal.
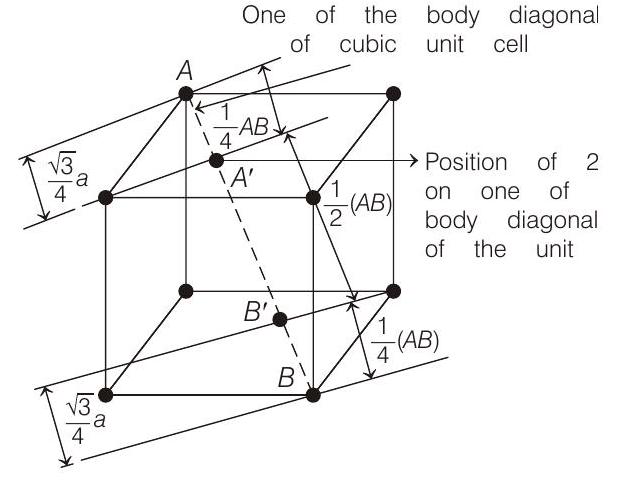
The angle between body diagonal and an edge is $\cos ^{-1}(1 / \sqrt{3})$. So, the projection of the line on an edge is $a / 4$. Similarly, other tetrahedral void also will be $a / 4$ away. So, the distance between these two is $\left[a-\frac{a}{4}\right]-\frac{a}{4}=\frac{a}{2}$.






