Solid State - Result Question 2
####2. An element has a face-centred cubic (fcc) structure with a cell edge of
(2019 Main, 12 April I)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 2. (c)
Solution:
- In fcc unit cell, two tetrahedral voids are formed on each of the four non-parallel body diagonals of the cube at a distance of
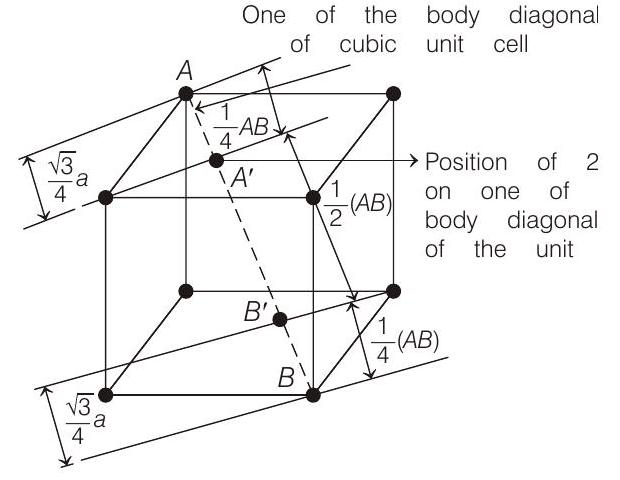
The angle between body diagonal and an edge is






