Solid State - Result Question 15
####15. $CsCl$ crystallises in body centred cubic lattice. If ’ $a$ ’ its edge length, then which of the following expressions is correct?
(a) $r _{Cs^{+}}+r _{Cl^{-}}=3 a$
(b) $r _{Cs^{+}}+r _{Cl^{-}}=\frac{3 a}{2}$
(c) $r _{Cs^{+}}+r _{Cl^{-}}=\frac{\sqrt{3}}{2} a$
(d) $r _{Cs^{+}}+r _{Cl^{-}}=\sqrt{3} a$
(2014 Main)
Show Answer
Answer:
Correct Answer: 15. (c)
Solution:
- In $CsCl, Cl^{-}$lies at corners of simple cube and $Cs^{+}$at the body centre. Hence, along the body diagonal, $Cs^{+}$and $Cl^{-}$touch each other so $r _{Cs^{+}}+r _{Cl^{-}}=2 r$
Calculation of $r$
In $\triangle E D F$,
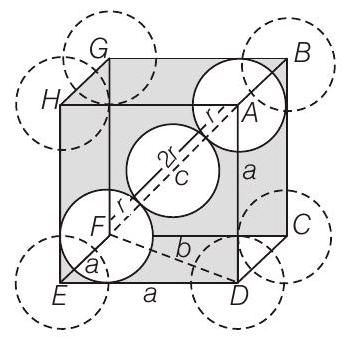
Body centred cubic unit cell
In $\triangle A F D$,
$$ F D=b=\sqrt{a^{2}+a^{2}}=\sqrt{2} a $$
$$ \begin{aligned} & c^{2}=a^{2}+b^{2}=a^{2}+(\sqrt{2} a)^{2}=a^{2}+2 a^{2} \\ & c^{2}=3 a^{2} \Rightarrow \quad c=\sqrt{3} a \end{aligned} $$
As $\triangle A F D$ is an equilateral triangle.
$$ \begin{array}{rlrl} & \therefore & \sqrt{3} a & =4 r \\ \Rightarrow & r & =\frac{\sqrt{3} a}{4} \\ & \text { Hence, } & r _{Cs^{+}}+r _{Cl^{-}} & =2 r=2 \times \frac{\sqrt{3}}{4} a=\frac{\sqrt{3}}{2} a \end{array} $$






